The Origin Destination(OD) Cost Matrix service helps you to create an OD cost matrix for multiple origins to multiple destinations. An OD cost matrix is a table that contains cost, such as travel time or travel distance, from each origin to each destination. Additionally, it ranks the destinations in ascending order based on the minimum cost required to travel. When generating an OD cost matrix, you can optionally specify the maximum number of destinations to find for each origin and the maximum time or distance to travel when searching for destinations.
By default, the matrix is generated with columns - origin id, destination id, destination rank, total time and total distance. In this sample notebook , we will use this tool to get OD matrix if given a set of origin and destination points, either as a csv with latitude and longitude or csv file with list of addresses. In later part of this sample, we will format the table to get n by n matrix.
This is useful when you want to solve other transportation problems with open source tools or heuristics. When it comes to real world TSP(Travelling Salesman Problem) or VRP(Vehicle Routing Problem) or other tranportation problems, data about travel time from every point to every other point can give you more realistic results than with euclidean distance.
Note :If you run the tutorial using ArcGIS Online, 0.003 credit will be consumed as there are 6 origin-destination pairs.
As a first step, let's import required libraries and establish a connection to your organization which could be an ArcGIS Online organization or an ArcGIS Enterprise. If you dont have an ArcGIS account, get ArcGIS Trial.
import arcgis
from arcgis.gis import GIS
import pandas as pd
import datetime
import getpass
from IPython.display import HTML
from arcgis import geocoding
from arcgis.features import Feature, FeatureSet
from arcgis.features import GeoAccessor, GeoSeriesAccessormy_gis = GIS('home')We will see how to create layer for origins and destinations when we have latitude and longitude and when we have addresses to geocode for converting to layer respectively.
Create origins layer:
We have latitude and longitude information for origins, with the following code snippet, we can create a layer from the information. We will reverse geocode the latitude longitude information to find the locations.
Note: Geocoding the addresses will consume credits.
origin_coords = ['-117.187807, 33.939479', '-117.117401, 34.029346']
origin_features = []
for origin in origin_coords:
reverse_geocode = geocoding.reverse_geocode({"x": origin.split(',')[0],
"y": origin.split(',')[1]})
origin_feature = Feature(geometry=reverse_geocode['location'],
attributes=reverse_geocode['address'])
origin_features.append(origin_feature)
origin_fset = FeatureSet(origin_features, geometry_type='esriGeometryPoint',
spatial_reference={'latestWkid': 4326})
origin_fset<FeatureSet> 2 features
Get destinations layer:
addresses_item = my_gis.content.search('destinations_address', 'feature layer')[0]
addresses_itemdestinations_sdf = addresses_item.layers[0].query(as_df=True)
destinations_sdf| Address | ObjectId | SHAPE | |
|---|---|---|---|
| 0 | 1151 W Lugonia Ave, Redlands, CA 92374 | 1 | {"x": -13046371.7016, "y": 4037983.0551000014,... |
| 1 | 1099 E Hospitality Ln, San Bernardino, CA 92408 | 2 | {"x": -13053662.5736, "y": 4037947.9793, "spat... |
| 2 | 4756, 120 E State St, Redlands, CA 92373 | 3 | {"x": -13044505.2086, "y": 4036358.3337000012,... |
destinations_fset = destinations_sdf.spatial.to_featureset()
destinations_fset<FeatureSet> 3 features
With these inputs, solve the problem with Origin Destintion matrix solver. Look up the doc to understand how this tool works and its parameters. Remember, 0.0005 credits per input origin and destination pair will be charged. For example, if there are 100 origins and 200 destinations, the cost will be 10 credits. If you specify a cutoff or limit the number of destinations, for instance, to find only 5 closest destinations within 10 minutes of every origin, the cost will still be 10 credits, as the credits depend on the number of input origin destination pairs.
TargetDestinationCount- The maximum number of destinations that must be found for the origin. If a value is not specified, the value from the Number of Destinations to Find parameter is used.
Cutoff- Specify the travel time or travel distance value at which to stop searching for destinations from the origin. Any destination beyond the cutoff value will not be considered. The value needs to be in the units specified by the Time Units parameter if the impedance attribute in your travel mode is time based or in the units specified by the Distance Units parameter if the impedance attribute in your travel mode is distance based. If a value is not specified, the tool will not enforce any travel time or travel distance limit when searching for destinations.
Specify origin_destination_line_shape to see the output in map. Even though the lines are straight for performance reasons, they always store the travel time and travel distance along the street network, not straight-line distance.
%%time
# solve OD cost matrix tool for the origns and destinations
from arcgis.network.analysis import generate_origin_destination_cost_matrix
results = generate_origin_destination_cost_matrix(origins= origin_fset, #origins_fc_latlong,
destinations= destinations_fset, #destinations_fs_address,
cutoff=200,
origin_destination_line_shape='Straight Line')
print('Analysis succeeded? {}'.format(results.solve_succeeded))Analysis succeeded? True CPU times: user 379 ms, sys: 27.1 ms, total: 406 ms Wall time: 24.7 s
Let's see the output lines table.
od_df = results.output_origin_destination_lines.sdf
od_df| DestinationOID | DestinationRank | OBJECTID | OriginOID | SHAPE | Shape_Length | Total_Distance | Total_Time | |
|---|---|---|---|---|---|---|---|---|
| 0 | 3 | 1 | 1 | 1 | {"paths": [[[-117.18779101399997, 33.939597752... | 0.117008 | 21.832442 | 24.159862 |
| 1 | 1 | 2 | 2 | 1 | {"paths": [[[-117.18779101399997, 33.939597752... | 0.130932 | 23.262677 | 24.910770 |
| 2 | 2 | 3 | 3 | 1 | {"paths": [[[-117.18779101399997, 33.939597752... | 0.149588 | 26.421002 | 27.939439 |
| 3 | 1 | 1 | 4 | 2 | {"paths": [[[-117.11711694599995, 34.028605892... | 0.091302 | 9.965429 | 7.510600 |
| 4 | 3 | 2 | 5 | 2 | {"paths": [[[-117.11711694599995, 34.028605892... | 0.069458 | 8.269718 | 8.067540 |
| 5 | 2 | 3 | 6 | 2 | {"paths": [[[-117.11711694599995, 34.028605892... | 0.151388 | 16.558662 | 13.764840 |
Convert to matrix format
We need to change the format to get a matrix with rows as origins and columns as destinations, with impedance value as travel time or travel distance. We will use the pivot_table feature of Pandas to accomplish that.
# filter only the required columns
od_df2 = od_df[['DestinationOID','OriginOID','Total_Distance','Total_Time']]
# user pivot_table
od_pivot = od_df2.pivot_table(index='OriginOID', columns='DestinationOID')
od_pivot| Total_Distance | Total_Time | |||||
|---|---|---|---|---|---|---|
| DestinationOID | 1 | 2 | 3 | 1 | 2 | 3 |
| OriginOID | ||||||
| 1 | 23.262677 | 26.421002 | 21.832442 | 24.91077 | 27.939439 | 24.159862 |
| 2 | 9.965429 | 16.558662 | 8.269718 | 7.51060 | 13.764840 | 8.067540 |
Write the pivot table to disk
od_pivot.to_csv('data/OD_Matrix.csv')This is how we can get OD cost matrix when we have csv files with origin and destinations location information. We could read this matrix and provide this as input to a heuristics or an open-source algorithm.
od_map = my_gis.map('Loma Linda, CA')
od_map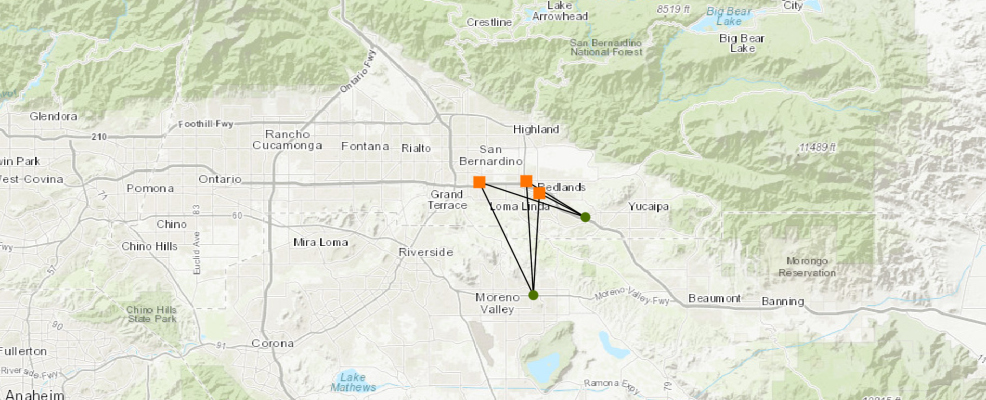
od_map.draw(results.output_origin_destination_lines)
od_map.draw(destinations_fset, symbol={"type": "esriSMS","style": "esriSMSSquare","color": [255,115,0,255], "size": 10})
od_map.draw(origin_fset, symbol={"type": "esriSMS","style": "esriSMSCircle","color": [76,115,0,255],"size": 8})Conclusion
This sample demonstrated how you can constuct an OD cost matrix using the Python API. We stared by defining 2 origin and 3 destination points. We used the generate_origin_destination_cost_matrix() method under the network module to compute the OD cost matrix.
How can you use this?
The OD cost matrix becomes an important analytical output for downstream routing and other network analysis problems. Imagine you run a pizza shop and receive orders for delivery in a central location. Based on the distance to these demand points, you need to decide which supply point (pizza shop) should service which demand point (customer address). You can solve problems such as these by computing the OD cost matrix.