Predictive Analysis of the 2019 Novel Coronavirus Pandemic

Introduction

Dashboards, statistics, and other information about the COVID-19 are floating all over the internet, and different countries or regions are adopting varied strategies, from complete lockdown, to social distancing, to herd immunity, you might be confused at what is the right strategy, and which information is valid. This notebook is not providing you a final answer, but tools or methods that you can try yourself in performing data modeling, analyzing, and predicting the spread of COVID-19 with the ArcGIS API for Python, and other libraries such as pandas and numpy. Hopefully, given the workflow demonstrations, you are able to find the basic facts, current patterns, and future trends behind the common notions about how COVID-19 spread from a dataset perspective [1,2,3,4].

Before we dive into data science and analytics, let's start with importing the necessary modules:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import time
from arcgis.gis import GIS

Import and Understand Source Dataset

Among all the official and unofficial data sources on the web providing COVID-19 related data, one of the most widely used dataset today is the one provided by the John Hopkins University's Center for Systems Science and Engineering (JHU CSSE), which can be accessed on GitHub under the name - Novel Coronavirus (COVID-19) Cases, provided by JHU CSSE [5,10,11,12]. The time-series consolidated data needed for all the analysis to be performed in this notebook fall into these two categories:

Type: Confirmed Cases, Deaths, and the Recovered;
Geography: Global, and the United States only.

Now let's first look at the U.S. dataset.

Time-series data for the United States

The dataset can be directly imported into data-frames with read_csv method in Pandas. Compared to downloading the file manually and then read it, it is preferred to use the URLs (which point to the CSV files archived on GitHub) because as situation changes, it becomes easier to load and refresh the analysis with new data.

Now, let's read the time-series data of the confirmed COVID-19 cases in the United States from the GitHub source url, into a Pandas DataFrame:

# read time-series csv
usa_ts_url = 'https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_US.csv'
usa_ts_df = pd.read_csv(usa_ts_url, header=0, escapechar='\\')
usa_ts_df.head(5)

	UID	iso2	iso3	code3	FIPS	Admin2	Province_State	Country_Region	Lat	Long_	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
0	16	AS	ASM	16	60.0	NaN	American Samoa	US	-14.2710	-170.1320	...	0	0	0	0	0	0	0	0	0	0
1	316	GU	GUM	316	66.0	NaN	Guam	US	13.4443	144.7937	...	247	247	247	253	257	267	280	280	280	280
2	580	MP	MNP	580	69.0	NaN	Northern Mariana Islands	US	15.0979	145.6739	...	30	30	30	30	30	30	31	31	31	31
3	630	PR	PRI	630	72.0	NaN	Puerto Rico	US	18.2208	-66.5901	...	6922	7066	7189	7250	7465	7537	7608	7683	7787	7916
4	850	VI	VIR	850	78.0	NaN	Virgin Islands	US	18.3358	-64.8963	...	81	81	81	81	81	90	92	98	111	111

5 rows × 177 columns

usa_ts_df.columns

Index(['UID', 'iso2', 'iso3', 'code3', 'FIPS', 'Admin2', 'Province_State',
       'Country_Region', 'Lat', 'Long_',
       ...
       '6/26/20', '6/27/20', '6/28/20', '6/29/20', '6/30/20', '7/1/20',
       '7/2/20', '7/3/20', '7/4/20', '7/5/20'],
      dtype='object', length=177)

As we can see from the printouts of usa_ts_df.columns, the first 11 columns are displayed as ['UID', 'iso2', 'iso3', 'code3', 'FIPS', 'Admin2', 'Province_State', 'Country_Region', 'Lat', 'Long_'], while the rest of the columns are dates from 1/22/20 to the most current date on record.

date_list = usa_ts_df.columns.tolist()[11:]
date_list[0], date_list[-1]

('1/22/20', '7/5/20')

Repair and Summarize the state-wide time-series data

Look at the last five rows of the DataFrame usa_ts_df, and see that they are all cases for Province_State=="Utah":

usa_ts_df.tail()

	UID	iso2	iso3	code3	FIPS	Admin2	Province_State	Country_Region	Lat	Long_	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
3256	84070016	US	USA	840	NaN	Central Utah	Utah	US	39.372319	-111.575868	...	127	134	143	159	169	173	180	194	201	209
3257	84070017	US	USA	840	NaN	Southeast Utah	Utah	US	38.996171	-110.701396	...	33	34	35	35	36	37	39	40	40	40
3258	84070018	US	USA	840	NaN	Southwest Utah	Utah	US	37.854472	-111.441876	...	1302	1361	1428	1467	1519	1553	1584	1625	1660	1689
3259	84070019	US	USA	840	NaN	TriCounty	Utah	US	40.124915	-109.517442	...	45	46	48	48	50	50	52	53	55	55
3260	84070020	US	USA	840	NaN	Weber-Morgan	Utah	US	41.271160	-111.914512	...	814	846	872	919	954	1004	1042	1090	1172	1195

5 rows × 177 columns

Some rows in the DataFrame are of many-rows-to-one-state matching, while others are of the one-row-to-one-state matching replationship. All records listed in the usa_ts_df with Admin2 not equal to NaN, are those rows that fall into the category of "many-rows-to-one-state" matching.

usa_ts_df[usa_ts_df["Admin2"].notna()].head()

	UID	iso2	iso3	code3	FIPS	Admin2	Province_State	Country_Region	Lat	Long_	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
5	84001001	US	USA	840	1001.0	Autauga	Alabama	US	32.539527	-86.644082	...	482	492	497	521	530	545	553	560	583	607
6	84001003	US	USA	840	1003.0	Baldwin	Alabama	US	30.727750	-87.722071	...	500	539	559	626	663	686	735	828	846	864
7	84001005	US	USA	840	1005.0	Barbour	Alabama	US	31.868263	-85.387129	...	309	314	314	319	322	323	333	345	347	349
8	84001007	US	USA	840	1007.0	Bibb	Alabama	US	32.996421	-87.125115	...	150	158	159	162	167	171	176	186	187	190
9	84001009	US	USA	840	1009.0	Blount	Alabama	US	33.982109	-86.567906	...	181	185	186	196	204	214	218	226	230	235

5 rows × 177 columns

As shown in the output of the previous two cells, we can see that for the usa_ts_df which we have created and parsed from the U.S. Dataset, there are multiple rows per state representing different administrative areas of the state with reported cases. Next, we will use the to-be-defined function sum_all_admins_in_state() to summarize all administrative areas in one state into a single row.

def sum_all_admins_in_state(df, state):
    
    # query all sub-records of the selected state
    tmp_df = df[df["Province_State"]==state]
    
    # create a new row which is to sum all statistics of this state, and 
    # assign the summed value of all sub-records to the date_time column of the new row
    sum_row = tmp_df.sum(axis=0)
    
    # assign the constants to the ['Province/State', 'Country/Region', 'Lat', 'Long'] columns; 
    # note that the Province/State column will be renamed from solely the country name to country name + ", Sum".
    sum_row.loc['UID'] = "NaN"
    sum_row.loc['Admin2'] = "NaN"
    sum_row.loc['FIPS'] = "NaN"
    sum_row.loc['iso2'] = "US"
    sum_row.loc['iso3'] = "USA"
    sum_row.loc['code3'] = 840
    sum_row.loc['Country_Region'] = "US"
    sum_row.loc['Province_State'] = state + ", Sum"
    sum_row.loc['Lat'] = tmp_df['Lat'].values[0]
    sum_row.loc['Long_'] = tmp_df['Long_'].values[0]
    
    # append the new row to the original DataFrame, and 
    # remove the sub-records of the selected country.
    df = pd.concat([df, sum_row.to_frame().T], ignore_index=True)
    #display(df[df["Province_State"].str.contains(state + ", Sum")])
    df=df[df['Province_State'] != state]
    df.loc[df.Province_State == state+", Sum", 'Province_State'] = state
    
    return df

# loop thru all states in the U.S.
for state in usa_ts_df.Province_State.unique():
    usa_ts_df = sum_all_admins_in_state(usa_ts_df, state)

Now with sum_all_admins_in_state applied to all states, we shall be expecting usa_ts_df to be with all rows converted to one-row-to-one-state matching. Let's browse the last five rows in the DataFrame to validate the results.

usa_ts_df.tail()

	UID	iso2	iso3	code3	FIPS	Admin2	Province_State	Country_Region	Lat	Long_	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
54	NaN	US	USA	840	NaN	NaN	West Virginia	US	39.1307	-80.0035	...	2730	2782	2832	2870	2905	2979	3053	3126	3205	3262
55	NaN	US	USA	840	NaN	NaN	Wisconsin	US	43.9697	-89.7678	...	26747	27286	27743	28058	28659	29199	29738	30317	31055	31577
56	NaN	US	USA	840	NaN	NaN	Wyoming	US	41.655	-105.724	...	1368	1392	1417	1450	1487	1514	1550	1582	1606	1634
57	NaN	US	USA	840	NaN	NaN	Diamond Princess	US	0	0	...	49	49	49	49	49	49	49	49	49	49
58	NaN	US	USA	840	NaN	NaN	Grand Princess	US	0	0	...	103	103	103	103	103	103	103	103	103	103

5 rows × 177 columns

Explore the state-wide time-series data

If you wonder in which state(s) the first COVID-19 case was confirmed and reported, use the cell below to check for first occurrence - in this case, the Washington State.

usa_ts_df_all_states = usa_ts_df.groupby('Province_State').sum()[date_list]
usa_ts_df_all_states[usa_ts_df_all_states['1/22/20']>0]

	1/22/20	1/23/20	1/24/20	1/25/20	1/26/20	1/27/20	1/28/20	1/29/20	1/30/20	1/31/20	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
Province_State
Washington	1	1	1	1	1	1	1	1	1	1	...	30855	31404	31752	32253	32824	33435	34151	34778	35247	35898

1 rows × 166 columns

Or if you want to query for the top 10 states with the highest numbers of confirmed cases for the time being, run the following cell to display the query results.

usa_ts_df_all_states[date_list[-1]].sort_values(ascending = False).head(10)

Province_State
New York         397131
California       264681
Florida          200111
Texas            194932
New Jersey       173402
Illinois         147251
Massachusetts    109974
Arizona           98103
Georgia           95516
Pennsylvania      94403
Name: 7/5/20, dtype: int64

Compared to what we have collected as the top 10 states on May 05, 2020, we can see California has climbed up to the 2nd place, while New Jersey rescinded to the 5th place.

Province_State
New York         321192
New Jersey       130593
Massachusetts     70271
Illinois          65889
California        58456
Pennsylvania      53864
Michigan          44451
Florida           37439
Texas             33912
Connecticut       30621
Name: 5/5/20, dtype: int64

The approach is quite similar if you want to query for the top 10 states with the lowest numbers of confirmed cases, just by simply changing the ascending order from False to True:

usa_ts_df_all_states[date_list[-1]].sort_values(ascending = True).head(10)

Province_State
American Samoa                 0
Northern Mariana Islands      31
Diamond Princess              49
Grand Princess               103
Virgin Islands               111
Guam                         280
Hawaii                      1023
Alaska                      1134
Montana                     1212
Vermont                     1249
Name: 7/5/20, dtype: int64

Comparatively, we can also check what is the difference against the statistics obtained on May 05, 2020 (as below),

Province_State
American Samoa                0
Northern Mariana Islands     14
Diamond Princess             49
Virgin Islands               66
Grand Princess              103
Guam                        145
Alaska                      371
Montana                     456
Wyoming                     604
Hawaii                      625
Name: 5/5/20, dtype: int64

As shown above, from May to July the state with the highest confirmed cases is the New York State, while the American Samoa is that of the lowest confirmed cases (as of 07/05/2020). Also, if you are only interested in finding out which state has the highest confirmed cases instead of the top 10, you can just run the cells below for an exact query result, and its time-series:

# state name, and the current number of confirmed
usa_ts_df_all_states[date_list[-1]].idxmax(), usa_ts_df_all_states[date_list[-1]].max()

('New York', 397131)

usa_ts_df[usa_ts_df['Province_State']=="New York"].sum()[date_list]

1/22/20         0
1/23/20         0
1/24/20         0
1/25/20         0
1/26/20         0
            ...  
7/1/20     394079
7/2/20     394954
7/3/20     395872
7/4/20     396598
7/5/20     397131
Length: 166, dtype: object

Map the confirmed cases per state

With the time-series DataFrame for the United States ready-to-use, we can then map the number of confirmed cases reported per state in a time-enabled manner. Next, we will see an animation being created from the end of January to Current:

gis = GIS('home', verify_cert=False)

"""Confirmed Cases per State shown on map widget"""
map0 = gis.map("US")
map0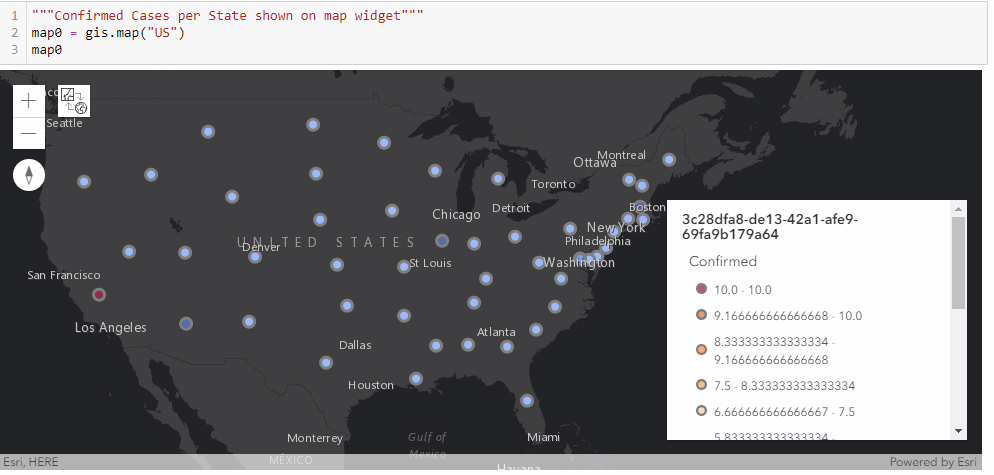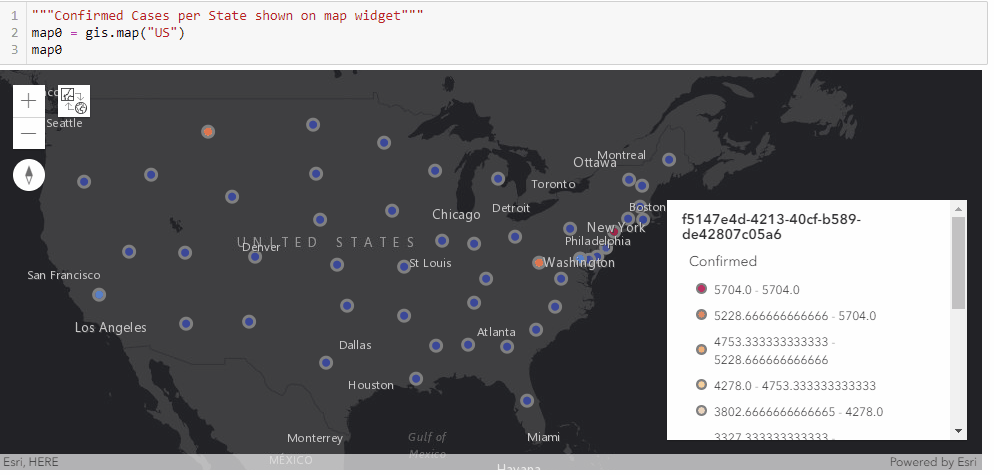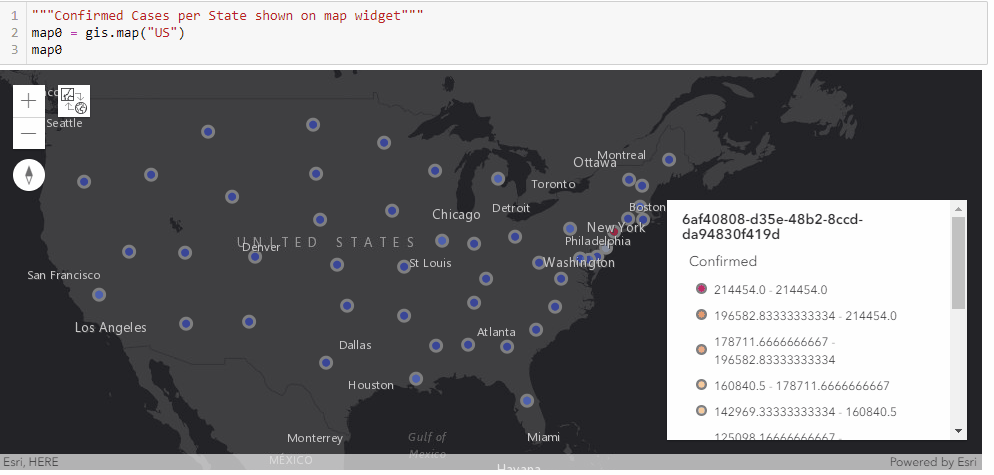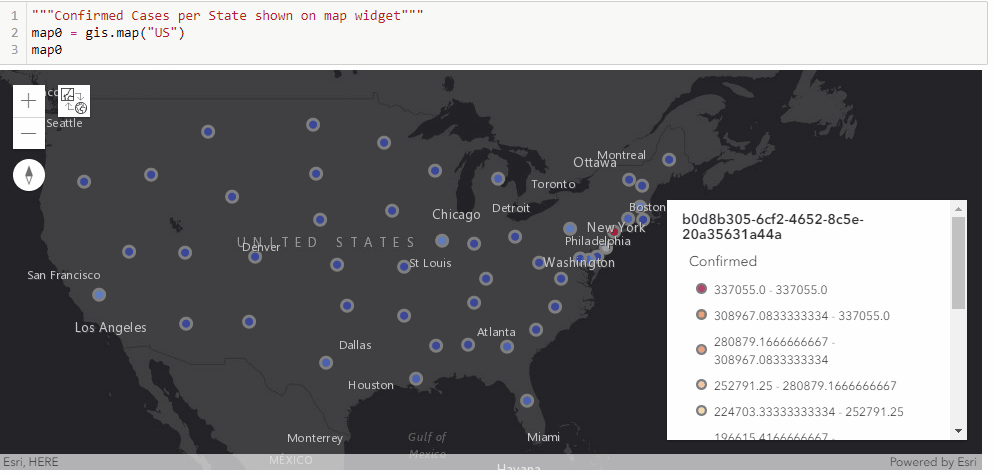

map0.basemap.basemap = "dark-gray-vector"
map0.zoom = 4

for d in date_list:
    map0.content.remove_all()
    map0.legend.enabled=False
    
    df = usa_ts_df[['Province_State', "Lat", "Long_", d]]
    df.rename(columns={d: 'Confirmed'}, inplace=True)

    fc = gis.content.import_data(df,
                                 {"Address":"Province_State"})
    fset=fc.query()
    fset.sdf.spatial.plot(map0)
    renderer_manager = map0.content.renderer(0)
    renderer_manager.smart_mapping().class_breaks_renderer(break_type="color", field="Confirmed", class_count=13, classification_method="natural-breaks")                     
    map0.legend.enabled=True
    time.sleep(3)

Chart the top 20 states with highest confirmed cases

Besides visualizing how the epicenter shifted from the West Coast to East Coast from previous animation, we can also show the evolution of the each state over time using a bar chart. Run the cell below to create an animation of how the top 20 states with highest confirmed cases in the U.S. changed during the pandemic:

from IPython.display import clear_output
import matplotlib.pyplot as plot

"""Chart the top 20 states with highest confirmed cases"""
time.sleep(3)
for d in date_list:
    clear_output(wait=True)
    top_20_per_d = usa_ts_df.groupby('Province_State')[['Province_State', d]].sum().sort_values(by=d, ascending=False).head(20)
    top_20_per_d.plot(kind='barh', log=True, figsize=(8,6))
    plt.ylabel("Province_State", labelpad=14)
    plt.xlabel("# of Confirmed Cases (log=True)", labelpad=14)
    plt.title("Chart the confirmed cases per state", y=1.02)
    plt.show()
    time.sleep(1)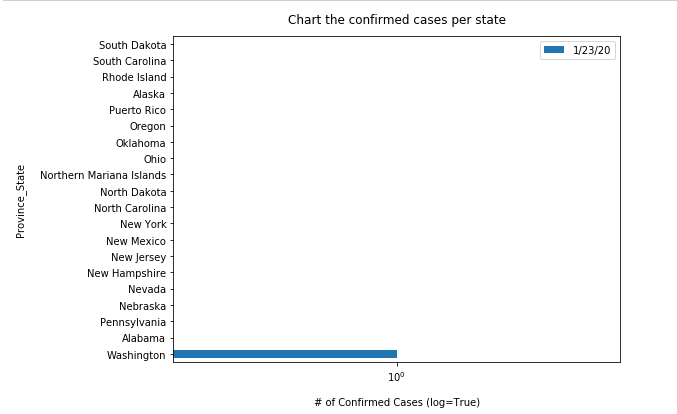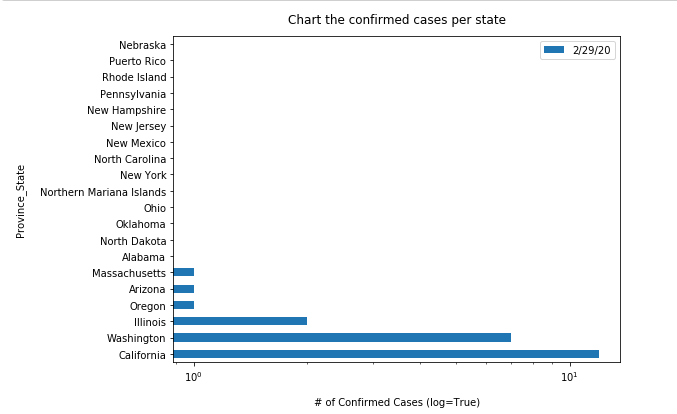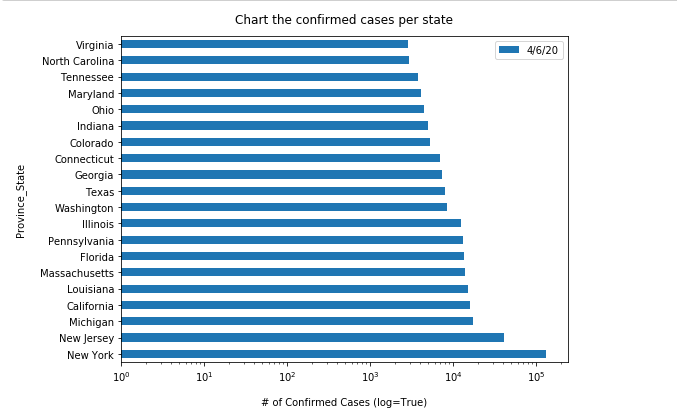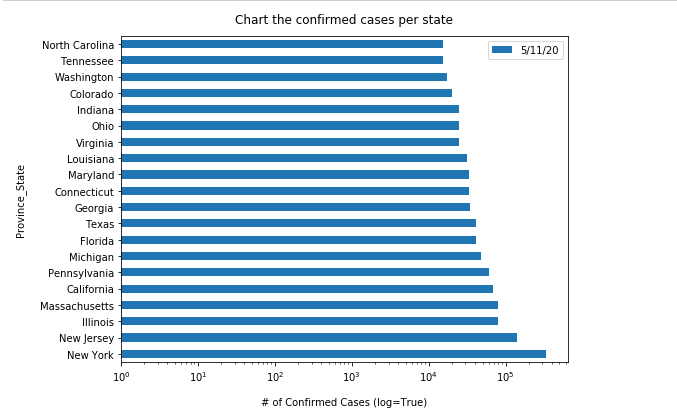

Time-series data at the country level around the world

Besides the U.S. dataset, we can also read the time-series data of the confirmed COVID-19 cases globally from the GitHub source url, into a Pandas DataFrame, again:

world_confirmed_ts_url = 'https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv'
world_confirmed_ts_df = pd.read_csv(world_confirmed_ts_url, header=0, escapechar='\\')
world_confirmed_ts_df.head(5)

	Province/State	Country/Region	Lat	Long	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
0	NaN	Afghanistan	33.0000	65.0000	...	30451	30616	30967	31238	31517	31836	32022	32324	32672	32951
1	NaN	Albania	41.1533	20.1683	...	2269	2330	2402	2466	2535	2580	2662	2752	2819	2893
2	NaN	Algeria	28.0339	1.6596	...	12685	12968	13273	13571	13907	14272	14657	15070	15500	15941
3	NaN	Andorra	42.5063	1.5218	...	855	855	855	855	855	855	855	855	855	855
4	NaN	Angola	-11.2027	17.8739	...	212	259	267	276	284	291	315	328	346	346

5 rows × 170 columns

Splitting records by different matching types

Though most of the rows in world_confirmed_ts_df DataFrame are the statistics at country-level (one-row-to-one-country matching), there are several countries listed in the DataFrame as an aggregation of provinces or states (many-rows-to-one-country matching). For instance, as shown below, the confirmed cases of Australia can be shown in the 8 rows printed.

world_confirmed_ts_df[world_confirmed_ts_df["Province/State"].notna()].head(8)

	Province/State	Country/Region	Lat	Long	1/26/20	1/27/20	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
8	Australian Capital Territory	Australia	-35.4735	149.0124	0	0	...	108	108	108	108	108	108	108	108	108	108
9	New South Wales	Australia	-33.8688	151.2093	3	4	...	3174	3177	3184	3189	3203	3211	3211	3405	3419	3429
10	Northern Territory	Australia	-12.4634	130.8456	0	0	...	29	29	29	29	29	30	30	30	30	30
11	Queensland	Australia	-28.0167	153.4000	0	0	...	1067	1067	1067	1067	1067	1067	1067	1067	1067	1067
12	South Australia	Australia	-34.9285	138.6007	0	0	...	440	440	440	443	443	443	443	443	443	443
13	Tasmania	Australia	-41.4545	145.9707	0	0	...	228	228	228	228	228	228	228	228	228	228
14	Victoria	Australia	-37.8136	144.9631	1	1	...	1947	2028	2099	2159	2231	2303	2368	2368	2536	2660
15	Western Australia	Australia	-31.9505	115.8605	0	0	...	608	609	609	611	611	611	611	611	612	618

8 rows × 170 columns

Browsing all the selected rows from above, we come to an conclusion that these five countries - Australia, Canada, China, Denmark, and France - are of the many-rows-to-one-country matching, and we need to summarize these rows into a single record, if such a row does not exist already. The following cell is to rule out the countries that are provided not only many-rows-to-one-country matching but also one-row-to-one-country matching.

for country in ["Australia", "Canada", "China", "Denmark", "France"]:
    df = world_confirmed_ts_df[world_confirmed_ts_df["Province/State"].isna()]
    df = df[df["Country/Region"]==country]
    if df.size:
        display(df)

	Province/State	Country/Region	Lat	Long	1/22/20	1/23/20	1/24/20	1/25/20	1/26/20	1/27/20	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
94	NaN	Denmark	56.2639	9.5018	0	0	0	0	0	0	...	12675	12675	12675	12751	12768	12794	12815	12832	12832	12832

1 rows × 170 columns

	Province/State	Country/Region	Lat	Long	1/22/20	1/23/20	1/24/20	1/25/20	1/26/20	1/27/20	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
116	NaN	France	46.2276	2.2137	0	0	2	3	3	3	...	193346	193152	192429	194109	194373	194985	195458	195904	195546	195535

1 rows × 170 columns

To summarize, we now can split the records into three matching types:

Countries with both many-rows-to-one-country matching and one-row-to-one-country matching data, e.g. Denmark, and France.
Countries with only many-rows-to-one-country matching data, e.g. Australia, Canada, and China.
Countries with only one-row-to-one-country matching data - rest of all countries in the DataFrame.

That being said, we would only need to summarize and repair the data for countries of type #2, which are Australia, Canada, and China.

Summarize and repair the time-series global confirmed cases

The method sum_all_provinces_in_country to be defined in the next cell performs these tasks:

query all sub-records of the selected country
create a new row which is to sum all statistics of this country, and assign the summed value of all sub-records to the date_time column of the new row
assign the constants to the ['Province/State', 'Country/Region', 'Lat', 'Long'] columns; note that the Country/Region column will be renamed from solely the country name to country name + ", Sum".
append the new row to the original DataFrame, and remove the sub-records of the selected country.

We will run the method against the subset of countries in type #2, which are Australia, Canada, and China.

def sum_all_provinces_in_country(df, country):
    
    # query all sub-records of the selected country
    tmp_df = df[df["Country/Region"]==country]
    
    # create a new row which is to sum all statistics of this country, and 
    # assign the summed value of all sub-records to the date_time column of the new row
    sum_row = tmp_df.sum(axis=0)
    
    # assign the constants to the ['Province/State', 'Country/Region', 'Lat', 'Long'] columns; 
    # note that the Country/Region column will be renamed from solely the country name to country name + ", Sum".
    sum_row.loc['Province/State'] = "NaN"
    sum_row.loc['Country/Region'] = country + ", Sum"
    sum_row.loc['Lat'] = tmp_df['Lat'].values[0]
    sum_row.loc['Long'] = tmp_df['Long'].values[0]
    
    # append the new row to the original DataFrame, and 
    # remove the sub-records of the selected country.
    df = pd.concat([df, sum_row.to_frame().T], ignore_index=True)
    display(df[df["Country/Region"].str.contains(country + ", Sum")])
    df=df[df['Country/Region'] != country]
    df.loc[df['Country/Region']== country+", Sum", 'Country/Region'] = country
    
    return df

for country in ["Australia", "Canada", "China"]:
    world_confirmed_ts_df = sum_all_provinces_in_country(world_confirmed_ts_df, country)

	Province/State	Country/Region	Lat	Long	1/22/20	1/23/20	1/24/20	1/25/20	1/26/20	1/27/20	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
266	NaN	Australia, Sum	-35.4735	149.012	0	0	0	0	4	5	...	7601	7686	7764	7834	7920	8001	8066	8260	8443	8583

1 rows × 170 columns

	Province/State	Country/Region	Lat	Long	1/22/20	1/23/20	1/24/20	1/25/20	1/26/20	1/27/20	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
259	NaN	Canada, Sum	53.9333	-116.576	0	0	0	0	1	1	...	104629	104878	105193	105830	106097	106288	106643	106962	107185	107394

1 rows × 170 columns

	Province/State	Country/Region	Lat	Long	1/22/20	1/23/20	1/24/20	1/25/20	1/26/20	1/27/20	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
246	NaN	China, Sum	31.8257	117.226	548	643	920	1406	2075	2877	...	84725	84743	84757	84780	84785	84816	84830	84838	84857	84871

1 rows × 170 columns

Now with the data summarized and repaired, we are good to query for the top 10 countries with the highest numbers of confirmed cases around the globe. You can choose to list the entire time-series for these 10 countries, or just pick the country/region name, and the most current statistics.

world_confirmed_ts_df.sort_values(by = date_list[-1], ascending = False).head(10)

	Province/State	Country/Region	Lat	Long	1/22/20	1/23/20	1/24/20	1/25/20	1/26/20	1/27/20	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
206	NaN	US	37.0902	-95.7129	1	1	2	2	5	5	...	2467554	2510259	2549294	2590668	2636414	2687588	2742049	2794153	2839436	2888635
20	NaN	Brazil	-14.235	-51.9253	0	0	0	0	0	0	...	1274974	1313667	1344143	1368195	1402041	1448753	1496858	1539081	1577004	1603055
112	NaN	India	21	78	0	0	0	0	0	0	...	508953	528859	548318	566840	585481	604641	625544	648315	673165	697413
168	NaN	Russia	60	90	0	0	0	0	0	0	...	619936	626779	633563	640246	646929	653479	660231	666941	673564	680283
162	NaN	Peru	-9.19	-75.0152	0	0	0	0	0	0	...	272364	275989	279419	282365	285213	288477	292004	295599	299080	302718
29	NaN	Chile	-35.6751	-71.543	0	0	0	0	0	0	...	263360	267766	271982	275999	279393	282043	284541	288089	291847	295532
204	NaN	United Kingdom	55.3781	-3.436	0	0	0	0	0	0	...	281675	282308	282703	283307	283710	283770	283774	284276	284900	285416
139	NaN	Mexico	23.6345	-102.553	0	0	0	0	0	0	...	208392	212802	216852	220657	226089	231770	238511	245251	252165	256848
182	NaN	Spain	40	-4	0	0	0	0	0	0	...	247905	248469	248770	248970	249271	249659	250103	250545	250545	250545
118	NaN	Italy	43	12	0	0	0	0	0	0	...	239961	240136	240310	240436	240578	240760	240961	241184	241419	241611

10 rows × 170 columns

# a simplified list
world_confirmed_ts_df[['Country/Region', date_list[-1]]].sort_values(by = date_list[-1], ascending = False).head(10)

	Country/Region	7/5/20
206	US	2888635
20	Brazil	1603055
112	India	697413
168	Russia	680283
162	Peru	302718
29	Chile	295532
204	United Kingdom	285416
139	Mexico	256848
182	Spain	250545
118	Italy	241611

That compared to the top 10 countries with confirmed COVID-19 cases we fetched and sorted on 03/23/2020, we can see how the list of countries changed.

Country_Region	Confirmed	Recovered	Deaths
China	81591	73280	3281
Italy	69176	8326	6820
United States	53660	0	703
Spain	39885	3794	2808
Germany	32986	3243	157
Iran	24811	8913	1934
France	22622	3288	1102
Switzerland	9877	131	122
South Korea	9037	3507	120
United Kingdom	8164	140	423

Table 1. The top 10 countries with confirmed COVID-19 cases collected at 03/23/2020.

Map the confirmed cases per country

Similar to the previous approach of mapping the confirmed cases in the United states through a timely evolutionary manner, here we are to visualize the confirmed cases per country/region along the timeline (from end of January to Current), and we shall be seeing the shift of epicenters from East Asia to North America in the animation.

As displayed in the legend, countries with the highest confirmed cases are to appear as red points, and the colormap changes from red to light blue and then to dark blue as the number of cases reduce.

"""Map the Confirmed Cases per country/region world-wide in the MapView"""
map1 = gis.map("Italy")
map1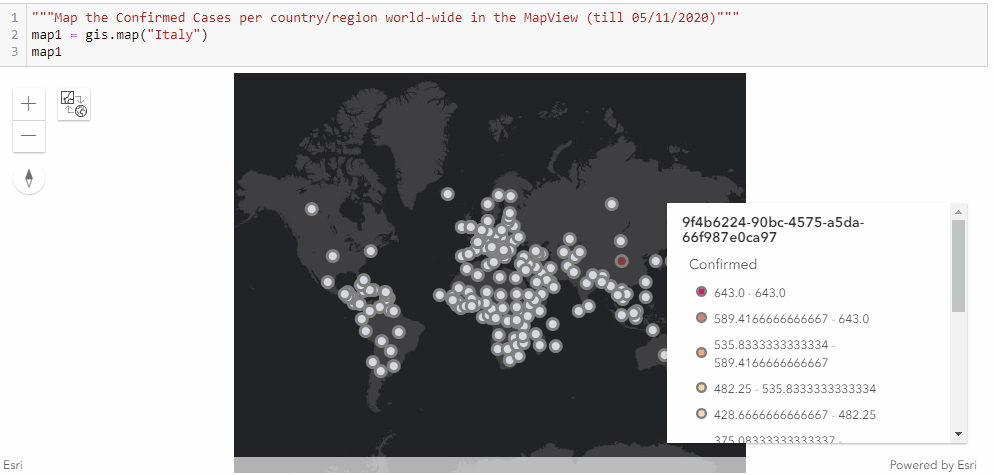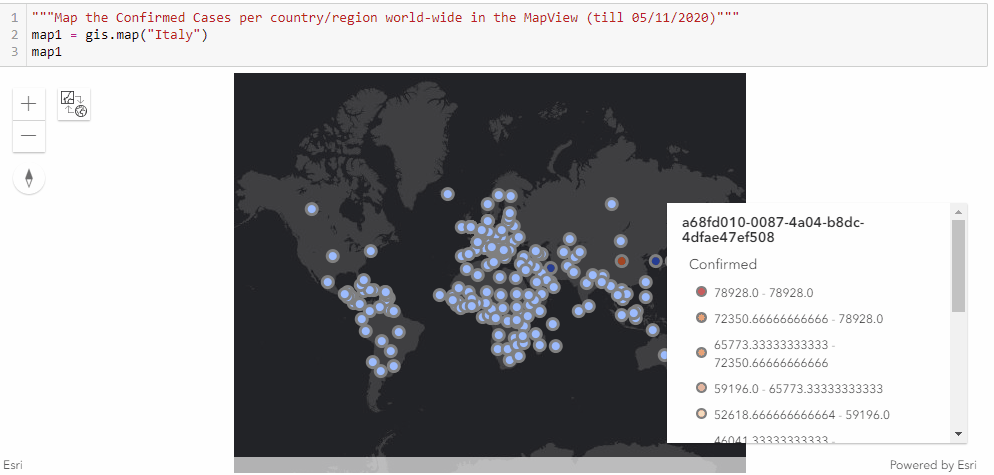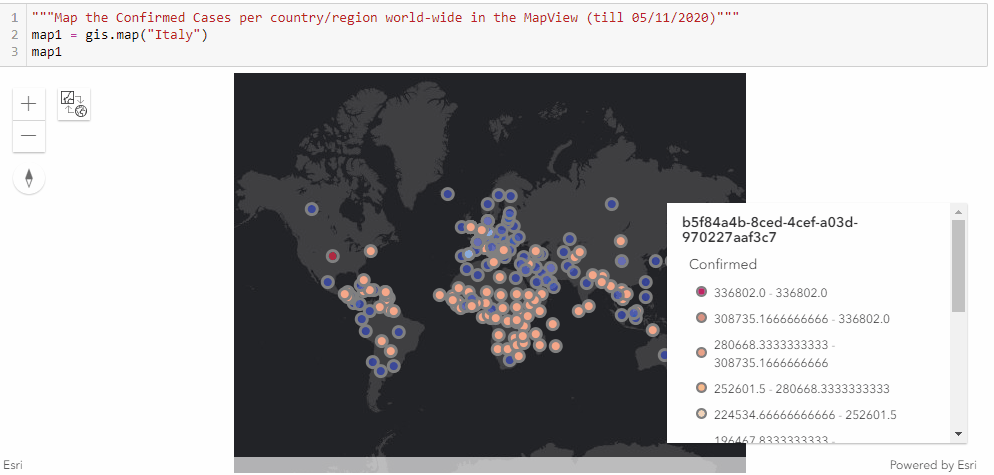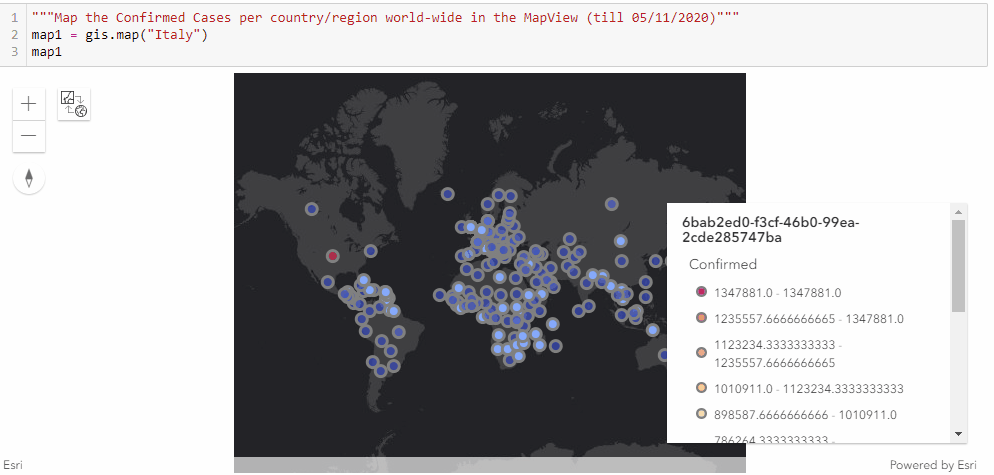

map1.basemap.basemap = "dark-gray-vector"
map1.zoom = 1

for d in date_list:
    map1.remove_layers()
    map1.legend.enabled=False
    
    df = world_confirmed_ts_df[['Country/Region', d]]
    df.rename(columns={d: 'Confirmed'}, inplace=True)
    fc = gis.content.import_data(df, 
                                 {"CountryCode":"Country_Region"},
                                 title="Confirmed cases per country of "+d)

    fset=fc.query()
    fset.sdf.spatial.plot(map1)
    renderer_manager = map1.content.renderer(0)
    renderer_manager.smart_mapping().class_breaks_renderer(break_type="color", field="Confirmed", class_count=13, classification_method="natural-breaks") 
    map1.legend.enabled=True
    time.sleep(3)

Chart the confirmed cases per country

Similarly, let us plot the top 20 countries with largest confirmed cases to be shown in vertical bar charts (in a time-enabled manner):

"""Chart the top 20 countries with highest confirmed cases"""
time.sleep(3)
for d in date_list:
    clear_output(wait=True)
    top_20_per_d = world_confirmed_ts_df.groupby('Country/Region')[['Country/Region', d]].sum().sort_values(by=d, ascending=False).head(20)
    top_20_per_d.plot(kind='barh', log=True, figsize=(8,6))
    plt.ylabel("Country/Region", labelpad=14)
    plt.xlabel("# of Confirmed Cases (log=True)", labelpad=14)
    plt.title("Chart the confirmed cases per country/region", y=1.02)
    plt.show()
    time.sleep(1)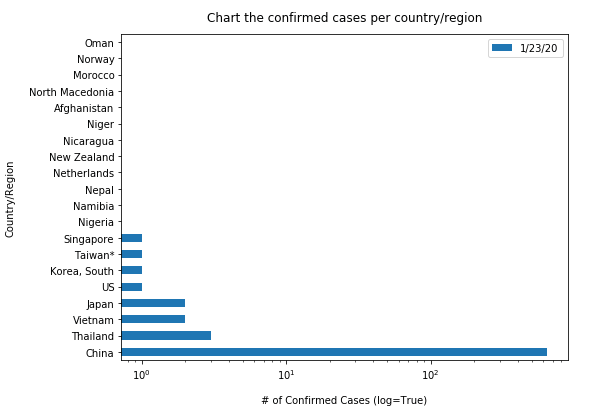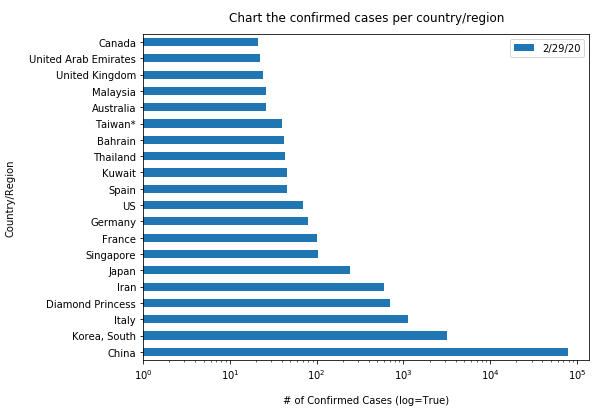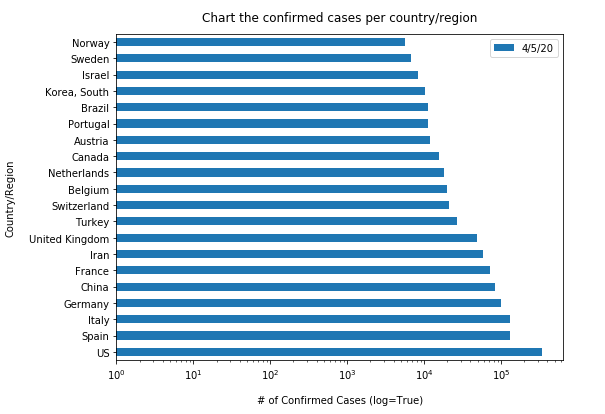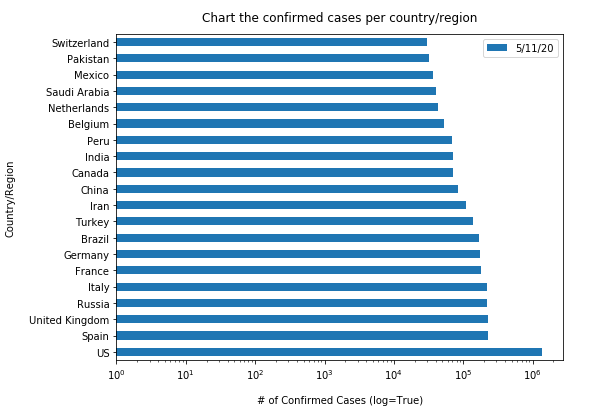

Summarize and repair the time-series COVID-19 deaths globally

Similar to what we have done in the previous section, we will perform the similar approach to fetch, parse and repair the data for COVID-19 deaths globally, which includes steps to:

fetch and read the online CSV source into DataFrame
summarize and repair the DataFrame
list the top 10 countries

world_deaths_ts_url = 'https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_deaths_global.csv'
world_deaths_ts_df = pd.read_csv(world_deaths_ts_url, header=0, escapechar='\\')
world_deaths_ts_df.head(5)

	Province/State	Country/Region	Lat	Long	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
0	NaN	Afghanistan	33.0000	65.0000	...	683	703	721	733	746	774	807	819	826	864
1	NaN	Albania	41.1533	20.1683	...	51	53	55	58	62	65	69	72	74	76
2	NaN	Algeria	28.0339	1.6596	...	885	892	897	905	912	920	928	937	946	952
3	NaN	Andorra	42.5063	1.5218	...	52	52	52	52	52	52	52	52	52	52
4	NaN	Angola	-11.2027	17.8739	...	10	10	11	11	13	15	17	18	19	19

5 rows × 170 columns

for country in ["Australia", "Canada", "China"]:
    world_deaths_ts_df = sum_all_provinces_in_country(world_deaths_ts_df, country)

	Province/State	Country/Region	Lat	Long	1/22/20	1/23/20	1/24/20	1/25/20	1/26/20	1/27/20	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
266	NaN	Australia, Sum	-35.4735	149.012	0	0	0	0	0	0	...	104	104	104	104	104	104	104	104	104	106

1 rows × 170 columns

	Province/State	Country/Region	Lat	Long	1/22/20	1/23/20	1/24/20	1/25/20	1/26/20	1/27/20	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
259	NaN	Canada, Sum	53.9333	-116.576	0	0	0	0	0	0	...	8571	8576	8582	8628	8650	8678	8700	8722	8732	8739

1 rows × 170 columns

	Province/State	Country/Region	Lat	Long	1/22/20	1/23/20	1/24/20	1/25/20	1/26/20	1/27/20	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
246	NaN	China, Sum	31.8257	117.226	17	18	26	42	56	82	...	4641	4641	4641	4641	4641	4641	4641	4641	4641	4641

1 rows × 170 columns

Now with the deaths statistics summarized and repaired, we are good to query for the top 10 countries with the highest numbers of COVID-19 deaths around the globe.

world_deaths_ts_df.sort_values(by = date_list[-1], ascending = False).head(10)

	Province/State	Country/Region	Lat	Long	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
206	NaN	US	37.0902	-95.7129	...	125631	126120	126360	126711	127432	128105	128803	129434	129676	129947
20	NaN	Brazil	-14.235	-51.9253	...	55961	57070	57622	58314	59594	60632	61884	63174	64265	64867
204	NaN	United Kingdom	55.3781	-3.436	...	43414	43514	43550	43575	43730	43906	43995	44131	44198	44220
118	NaN	Italy	43	12	...	34708	34716	34738	34744	34767	34788	34818	34833	34854	34861
139	NaN	Mexico	23.6345	-102.553	...	25779	26381	26648	27121	27769	28510	29189	29843	30366	30639
97	NaN	France	46.2276	2.2137	...	29705	29704	29704	29736	29763	29780	29794	29812	29812	29813
182	NaN	Spain	40	-4	...	28338	28341	28343	28346	28355	28364	28368	28385	28385	28385
112	NaN	India	21	78	...	15685	16095	16475	16893	17400	17834	18213	18655	19268	19693
114	NaN	Iran	32	53	...	10239	10364	10508	10670	10817	10958	11106	11260	11408	11571
162	NaN	Peru	-9.19	-75.0152	...	8939	9135	9317	9504	9677	9860	10045	10226	10412	10589

10 rows × 170 columns

# a simplified view
world_deaths_ts_df[['Country/Region', date_list[-1]]].sort_values(by = date_list[-1], ascending = False).head(10)

	Country/Region	7/5/20
206	US	129947
20	Brazil	64867
204	United Kingdom	44220
118	Italy	34861
139	Mexico	30639
97	France	29813
182	Spain	28385
112	India	19693
114	Iran	11571
162	Peru	10589

Summarize and repair the time-series global recovered cases

Like what we have done in the previous sections, we will perform the similar approach to fetch, parse and repair the data for global recovered cases, which includes steps to:

fetch and read the online CSV source into DataFrame
summarize and repair the DataFrame
list the top 10 countries

world_recovered_ts_url = 'https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_recovered_global.csv'
world_recovered_ts_df = pd.read_csv(world_recovered_ts_url, header=0, escapechar='\\')
world_recovered_ts_df.head(5)

	Province/State	Country/Region	Lat	Long	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
0	NaN	Afghanistan	33.0000	65.0000	...	10306	10674	12604	13934	14131	15651	16041	17331	19164	19366
1	NaN	Albania	41.1533	20.1683	...	1298	1346	1384	1438	1459	1516	1559	1592	1637	1657
2	NaN	Algeria	28.0339	1.6596	...	9066	9202	9371	9674	9897	10040	10342	10832	11181	11492
3	NaN	Andorra	42.5063	1.5218	...	799	799	799	799	799	799	800	800	800	800
4	NaN	Angola	-11.2027	17.8739	...	81	81	81	93	93	97	97	107	108	108

5 rows × 170 columns

for country in ["Australia", "Canada", "China"]:
    world_recovered_ts_df = sum_all_provinces_in_country(world_recovered_ts_df, country)

	Province/State	Country/Region	Lat	Long	1/22/20	1/23/20	1/24/20	1/25/20	1/26/20	1/27/20	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
253	NaN	Australia, Sum	-35.4735	149.012	0	0	0	0	0	0	...	6960	6993	7007	7037	7040	7090	7130	7319	7399	7420

1 rows × 170 columns

	Province/State	Country/Region	Lat	Long	1/22/20	1/23/20	1/24/20	1/25/20	1/26/20	1/27/20	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
246	NaN	Canada, Sum	56.1304	-106.347	0	0	0	0	0	0	...	67182	67445	67689	68698	69120	69397	69872	70232	70507	70772

1 rows × 170 columns

	Province/State	Country/Region	Lat	Long	1/22/20	1/23/20	1/24/20	1/25/20	1/26/20	1/27/20	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
246	NaN	China, Sum	31.8257	117.226	28	30	36	39	49	58	...	79580	79591	79609	79619	79632	79650	79665	79680	79706	79718

1 rows × 170 columns

Now with the statistics summarized and repaired, we are good to query for the top 10 countries with the highest numbers of COVID-19 recovered cases around the globe.

world_recovered_ts_df.sort_values(by = date_list[-1], ascending = False).head(10)

	Province/State	Country/Region	Lat	Long	...	6/26/20	6/27/20	6/28/20	6/29/20	6/30/20	7/1/20	7/2/20	7/3/20	7/4/20	7/5/20
21	NaN	Brazil	-14.235	-51.9253	...	702399	727715	746018	757811	788318	817642	957692	984615	990731	1029045
216	NaN	US	37.0902	-95.7129	...	670809	679308	685164	705203	720631	729994	781970	790404	894325	906763
175	NaN	Russia	60	90	...	383524	392703	398436	402778	411973	422235	428276	437155	446127	449995
116	NaN	India	21	78	...	295881	309713	321723	334822	347912	359860	379892	394227	409083	424433
30	NaN	Chile	-35.6751	-71.543	...	223431	228055	232210	236154	241229	245443	249247	253343	257451	261039
118	NaN	Iran	32	53	...	177852	180661	183310	186180	188758	191487	194098	196446	198949	201330
145	NaN	Mexico	23.6345	-102.553	...	156827	160721	164646	170147	174538	178526	183757	189345	195724	199914
169	NaN	Peru	-9.19	-75.0152	...	159806	164024	167998	171159	174535	178245	182097	185852	189621	193957
122	NaN	Italy	43	12	...	187615	188584	188891	189196	190248	190717	191083	191467	191944	192108
103	NaN	Germany	51	9	...	177149	177518	177657	177770	178100	179100	179800	180300	181000	181719

10 rows × 170 columns

# a simplfied view
world_recovered_ts_df[['Country/Region', date_list[-1]]].sort_values(by = date_list[-1], ascending = False).head(10)

	Country/Region	7/5/20
21	Brazil	1029045
216	US	906763
175	Russia	449995
116	India	424433
30	Chile	261039
118	Iran	201330
145	Mexico	199914
169	Peru	193957
122	Italy	192108
103	Germany	181719

Enough with understanding, summarizing, and exploratory analysis on the the existing data, now let us model the data on the Polynomial Regression, Neural Network, and SIR epidemic models and try to predict the count of cases in the upcoming days.

Predictive Analysis

Before performing the predictive analysis using the time-series data for the United States, we first need to transpose the time-series matrix, and map the date fields into number of days since the first reported. In the following, we will perform the approach three times to make three new analysis-ready DataFrames, namely, new_usa_confirmed_df, new_usa_deaths_df, and new_usa_recovered_df [15,16,17,18].

usa_overall_confirmed_ts_df = world_confirmed_ts_df[world_confirmed_ts_df["Country/Region"] == "US"]
new_usa_confirmed_df = usa_overall_confirmed_ts_df[date_list].T
new_usa_confirmed_df.columns = ["confirmed"]
new_usa_confirmed_df = new_usa_confirmed_df.assign(days=[1 + 
                                               i for i in range(len(new_usa_confirmed_df))])[['days'] + 
                                               new_usa_confirmed_df.columns.tolist()]
new_usa_confirmed_df

	days	confirmed
1/22/20	1	1
1/23/20	2	1
1/24/20	3	2
1/25/20	4	2
1/26/20	5	5
...	...	...
6/30/20	161	2636414
7/1/20	162	2687588
7/2/20	163	2742049
7/3/20	164	2794153
7/4/20	165	2839436

165 rows × 2 columns

usa_overall_deaths_ts_df = world_deaths_ts_df[world_deaths_ts_df["Country/Region"] == "US"]
new_usa_deaths_df = usa_overall_deaths_ts_df[date_list].T
new_usa_deaths_df.columns = ["deaths"]
new_usa_deaths_df = new_usa_deaths_df.assign(days=[1 +
                                                   i for i in range(len(new_usa_deaths_df))])[['days'] + 
                                                   new_usa_deaths_df.columns.tolist()]
new_usa_deaths_df

	days	deaths
1/22/20	1	0
1/23/20	2	0
1/24/20	3	0
1/25/20	4	0
1/26/20	5	0
...	...	...
6/30/20	161	127432
7/1/20	162	128105
7/2/20	163	128803
7/3/20	164	129434
7/4/20	165	129676

165 rows × 2 columns

usa_overall_recovered_ts_df = world_recovered_ts_df[world_recovered_ts_df["Country/Region"] == "US"]
new_usa_recovered_df = usa_overall_recovered_ts_df[date_list].T
new_usa_recovered_df.columns = ["recovered"]
new_usa_recovered_df = new_usa_recovered_df.assign(days=[1 +
                                                         i for i in range(len(new_usa_recovered_df))])[['days'] + 
                                                         new_usa_recovered_df.columns.tolist()]
new_usa_recovered_df

	days	recovered
1/22/20	1	0
1/23/20	2	0
1/24/20	3	0
1/25/20	4	0
1/26/20	5	0
...	...	...
6/30/20	161	720631
7/1/20	162	729994
7/2/20	163	781970
7/3/20	164	790404
7/4/20	165	894325

165 rows × 2 columns

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures

class PolynomialRegressionModel:

    def __init__(self, model_name, polynomial_degree):
        self.__model_name = model_name
        self.__polynomial_degree = polynomial_degree
        self.__model = None

    def train(self, x, y):
        polynomial_features = PolynomialFeatures(degree=self.__polynomial_degree)
        x_poly = polynomial_features.fit_transform(x)
        self.__model = LinearRegression()
        self.__model.fit(x_poly, y)

    def get_predictions(self, x):
        polynomial_features = PolynomialFeatures(degree=self.__polynomial_degree)
        x_poly = polynomial_features.fit_transform(x)
        return np.round(self.__model.predict(x_poly), 0).astype(np.int32)

    def get_model_polynomial_str(self):
        coef = self.__model.coef_
        intercept = self.__model.intercept_
        poly = "{0:.3f}".format(intercept)

        for i in range(1, len(coef)):
            if coef[i] >= 0:
                poly += " + "
            else:
                poly += " - "
            poly += "{0:.3f}".format(coef[i]).replace("-", "") + "X^" + str(i)

        return poly

training_set = new_usa_confirmed_df
x = np.array(training_set["days"]).reshape(-1, 1)
y = training_set["confirmed"]

training_set_deaths = new_usa_deaths_df
x_deaths = np.array(training_set_deaths["days"]).reshape(-1, 1)
y_deaths = training_set_deaths["deaths"]

Polynomial Regression

Let us first try to fit the data with a Polynomial Regression model, since the time-series chart of confirmed cases looks like an exponential curve:

Confirmed Cases with PR model

degrees = 2

regression_model = PolynomialRegressionModel("Cases using Polynomial Regression", 2)
regression_model.train(x, y)

y_pred = regression_model.get_predictions(x)
y_pred

array([ -68133,  -70086,  -71795,  -73260,  -74481,  -75456,  -76188,
        -76674,  -76917,  -76915,  -76668,  -76177,  -75442,  -74462,
        -73237,  -71768,  -70055,  -68097,  -65894,  -63447,  -60756,
        -57820,  -54640,  -51215,  -47546,  -43632,  -39474,  -35071,
        -30424,  -25532,  -20396,  -15016,   -9390,   -3521,    2593,
          8952,   15555,   22402,   29494,   36831,   44412,   52237,
         60307,   68621,   77180,   85983,   95031,  104323,  113860,
        123641,  133667,  143937,  154452,  165211,  176214,  187463,
        198955,  210692,  222674,  234900,  247370,  260085,  273045,
        286248,  299697,  313390,  327327,  341509,  355935,  370606,
        385521,  400681,  416085,  431734,  447627,  463764,  480147,
        496773,  513644,  530760,  548120,  565724,  583573,  601667,
        620005,  638587,  657414,  676485,  695801,  715361,  735166,
        755216,  775509,  796048,  816830,  837857,  859129,  880645,
        902406,  924411,  946660,  969155,  991893, 1014876, 1038104,
       1061576, 1085292, 1109253, 1133458, 1157908, 1182602, 1207541,
       1232725, 1258152, 1283825, 1309741, 1335903, 1362308, 1388958,
       1415853, 1442992, 1470376, 1498004, 1525876, 1553994, 1582355,
       1610961, 1639811, 1668906, 1698246, 1727830, 1757658, 1787731,
       1818048, 1848610, 1879416, 1910467, 1941762, 1973302, 2005086,
       2037115, 2069388, 2101906, 2134668, 2167675, 2200926, 2234421,
       2268161, 2302146, 2336375, 2370848, 2405566, 2440528, 2475735,
       2511187, 2546883, 2582823, 2619008, 2655437, 2692111, 2729029,
       2766192, 2803599, 2841250, 2879147])

def print_forecast(model_name, model, beginning_day=0, limit=10):

    next_days_x = np.array(range(beginning_day, beginning_day + limit)).reshape(-1, 1)
    next_days_pred = model.get_predictions(next_days_x)

    print("The forecast for " + model_name + " in the following " + str(limit) + " days is:")
    for i in range(0, limit):
        print("Day " + str(i + 1) + ": " + str(next_days_pred[i]))

print_forecast("Cases using Polynomial Regression", regression_model, 
               beginning_day=len(x), 
               limit=10)

The forecast for Cases using Polynomial Regression in the following 10 days is:
Day 1: 2879147
Day 2: 2917287
Day 3: 2955672
Day 4: 2994302
Day 5: 3033176
Day 6: 3072294
Day 7: 3111657
Day 8: 3151265
Day 9: 3191117
Day 10: 3231213

import operator

def plot_graph(model_name, x, y, y_pred):

    plt.scatter(x, y, s=10)
    sort_axis = operator.itemgetter(0)
    sorted_zip = sorted(zip(x, y_pred), key=sort_axis)
    x, y_pred = zip(*sorted_zip)

    plt.plot(x, y_pred, color='m')
    plt.title("Amount of " + model_name + " in each day")
    plt.xlabel("Day")
    plt.ylabel(model_name)
    plt.show()

plot_graph("Cases using Polynomial Regression", x, y, y_pred)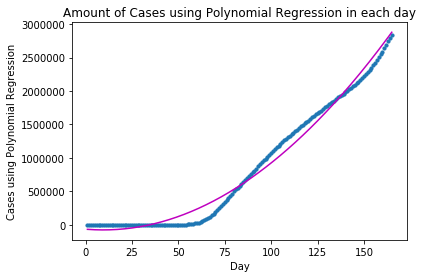

The approximation between the fitted and the actual curves does not look too ideal. We can then increase the degree of the Polynomial Regression Model to 3, and see what happens:

degrees = 3

regression_model = PolynomialRegressionModel("Confirmed cases using Polynomial Regression (d=3)", 3)
regression_model.train(x, y)
y_pred = regression_model.get_predictions(x)
print_forecast("Confirmed cases using Polynomial Regression (d=3)", regression_model, 
               beginning_day=len(x), 
               limit=10)
plot_graph("Confirmed cases using Polynomial Regression (d=3)", x, y, y_pred)

The forecast for Confirmed cases using Polynomial Regression (d=3) in the following 10 days is:
Day 1: 2664083
Day 2: 2685999
Day 3: 2707664
Day 4: 2729074
Day 5: 2750221
Day 6: 2771100
Day 7: 2791706
Day 8: 2812031
Day 9: 2832070
Day 10: 2851818

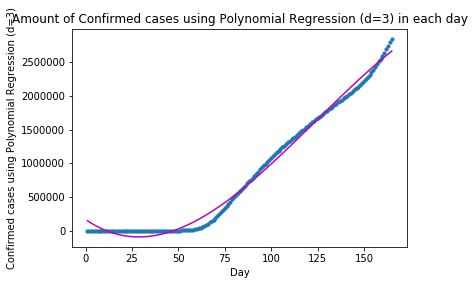
Though the approximation of the fitted curve and the actual data got improved for when days<80, the two curves diverged towards days=100.

The same approach can be done with the death cases using Polynomial Regression model (degree=2, and 3):

Deaths with PR

Degrees = 2

regression_model = PolynomialRegressionModel("Deaths using Polynomial Regression", 2)
regression_model.train(x_deaths, y_deaths)
y_deaths_pred = regression_model.get_predictions(x_deaths)
print_forecast("Deaths using Polynomial Regression", regression_model, 
               beginning_day=len(x_deaths), 
               limit=10)
plot_graph("Deaths using Polynomial Regression", x_deaths, y_deaths, y_deaths_pred)

The forecast for Deaths using Polynomial Regression in the following 10 days is:
Day 1: 152437
Day 2: 154332
Day 3: 156237
Day 4: 158153
Day 5: 160081
Day 6: 162020
Day 7: 163970
Day 8: 165930
Day 9: 167902
Day 10: 169885

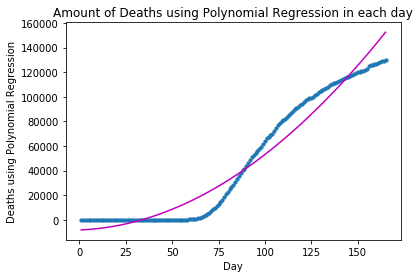
regression_model = PolynomialRegressionModel("Deaths using Polynomial Regression (d=3)", 3)
regression_model.train(x_deaths, y_deaths)
y_deaths_pred = regression_model.get_predictions(x_deaths)
print_forecast("Deaths using Polynomial Regression (d=3)", regression_model, 
               beginning_day=len(x_deaths), 
               limit=10)
plot_graph("Deaths using Polynomial Regression (d=3)", x_deaths, y_deaths, y_deaths_pred)

The forecast for Deaths using Polynomial Regression (d=3) in the following 10 days is:
Day 1: 129623
Day 2: 129797
Day 3: 129928
Day 4: 130018
Day 5: 130065
Day 6: 130069
Day 7: 130029
Day 8: 129945
Day 9: 129815
Day 10: 129639

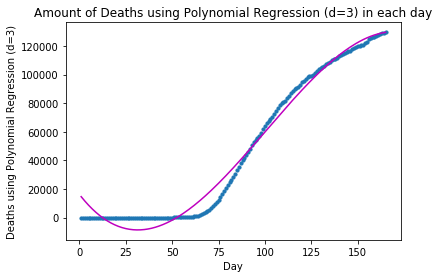
Since the model fitting results we have obtained so far with Polynomial Regression (degrees=2, and 3) are not too ideal, let us turn to Neural Network modeling and see whether its result would be better:

Neural Network

Confirmed Cases with NN

from sklearn.neural_network import MLPRegressor

class NeuralNetModel:

    def __init__(self, model_name):
        self.__model_name = model_name
        self.__model = None

    def train(self, x, y, hidden_layer_sizes=[10,], learning_rate=0.001, max_iter=2000):
        self.__model = MLPRegressor(solver="adam", activation="relu", alpha=1e-5, random_state=0, 
                                    hidden_layer_sizes=hidden_layer_sizes, verbose=False, tol=1e-5, 
                                    learning_rate_init=learning_rate, max_iter=max_iter)
        self.__model.fit(x, y)

    def get_predictions(self, x):
        return np.round(self.__model.predict(x), 0).astype(np.int32)

neural_net_model = NeuralNetModel("Confirmed Cases using Neural Network")
neural_net_model.train(x, y, [80, 80], 0.001, 50000)

y_pred = neural_net_model.get_predictions(x)
y_pred

array([  -2452,    -386,    1681,    3748,    5812,    6725,    5716,
          4642,    3569,    2495,    1421,     347,    -726,   -1800,
         -2874,   -3947,   -2357,   -2283,   -2228,   -2177,   -2213,
         -2250,   -2287,   -2323,   -2360,   -2397,   -2434,   -2470,
         -2507,   -2544,   -2580,   -2617,   -2654,   -2691,   -2727,
         -2764,   -2801,   -2837,   -2874,   -2911,   -2948,   -2984,
         -3021,   -2152,   -1039,      74,    1187,    2300,    3414,
          4527,    5640,    6753,    7866,    8979,   10092,   11205,
         12318,   13432,   14545,   15658,   28702,   49546,   70389,
         95895,  121508,  147121,  172734,  198347,  223961,  249574,
        275187,  300800,  326414,  352027,  377640,  403253,  428867,
        454480,  480093,  505706,  531320,  556933,  582546,  608159,
        633772,  659386,  684999,  710612,  736225,  761839,  787452,
        813065,  838678,  864292,  889905,  915518,  941131,  966745,
        992358, 1017971, 1043584, 1069197, 1094811, 1120424, 1146037,
       1171650, 1197264, 1222877, 1248490, 1274103, 1299717, 1325330,
       1350943, 1376556, 1402170, 1427783, 1453396, 1479009, 1504622,
       1530236, 1555849, 1581462, 1607075, 1632689, 1658302, 1683915,
       1709528, 1735142, 1760755, 1786368, 1811981, 1837595, 1863208,
       1888821, 1914434, 1940047, 1965661, 1991274, 2016887, 2042500,
       2068114, 2093727, 2119340, 2144953, 2170567, 2196180, 2221793,
       2247406, 2273019, 2298633, 2324246, 2349859, 2375472, 2401086,
       2426699, 2452312, 2477925, 2503539, 2529152, 2554765, 2580378,
       2605992, 2631605, 2657218, 2682831])

print_forecast("Confirmed Cases using Neural Network", neural_net_model, 
               beginning_day=len(x), 
               limit=10)

The forecast for Confirmed Cases using Neural Network in the following 10 days is:
Day 1: 2682831
Day 2: 2708305
Day 3: 2732643
Day 4: 2756752
Day 5: 2780861
Day 6: 2804970
Day 7: 2829079
Day 8: 2853188
Day 9: 2877298
Day 10: 2901407

plot_graph("Confirmed Cases using Neural Network", x, y, y_pred)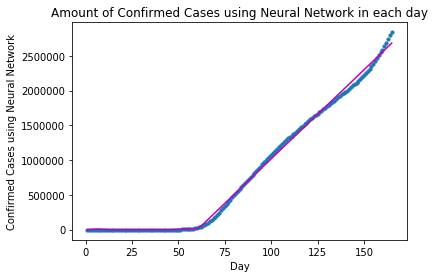

Deaths with NN

neural_net_model = NeuralNetModel("Deaths using Neural Network")
neural_net_model.train(x_deaths, y_deaths, [100, 100], 0.001, 50000)
y_deaths_pred = neural_net_model.get_predictions(x_deaths)
print_forecast("Deaths using Neural Network", neural_net_model, 
               beginning_day=len(x_deaths), 
               limit=10)
plot_graph("Deaths using Neural Network", x_deaths, y_deaths, y_deaths_pred)

The forecast for Deaths using Neural Network in the following 10 days is:
Day 1: 133677
Day 2: 134568
Day 3: 135459
Day 4: 136350
Day 5: 137241
Day 6: 138132
Day 7: 139023
Day 8: 139914
Day 9: 140805
Day 10: 141696

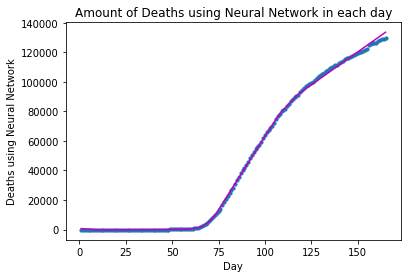
For Neural Network modeling, the approximation between the fitted and the actual curves looks much better than that of Polynomial Regression.

To summarize, the predicted numbers for the confirmed cases and deaths for the next 10 days (as of EOD 07/14/2020) in the United States are different with varied models:

Model	Confirmed	Deaths	Death Rate
PR (d=2)	3,231,213	169,885	5.26%
PR (d=3)	2,851,818	129,639	4.55%
NN	2,901,407	141,696	4.88%

Table 2. The predicted numbers for the confirmed cases and deaths for the next 10 days (as of EOD 07/14/2020).

SIR Model

The Polynomial Regression and Neural Network models used in the previous section did provide reasonable predictions to the confirmed and death numbers in upcoming days. However, these models did not consider the nature of infectious diseases in between the figures. Next, we will talk about how Compartmental Modeling techniques can be used to model infectious diseases (and in this case, the COVID-19), of which the simplest compartmental model is the SIR model. You can check out the descriptions to the model and its basic blocks in the Wiki Page here. The SIR model is reasonably predictive for infectious diseases which are transmitted from human to human, and where recovery confers lasting resistance, such as measles, mumps and rubella [6,7,8,9].

As we can tell from the name of the model, it consists of three compartments: S for the number of susceptible, I for the number of infectious, and R for the number of recovered or deceased (or immune) individuals. Each member of the population typically progresses from susceptible to infectious to recovered.

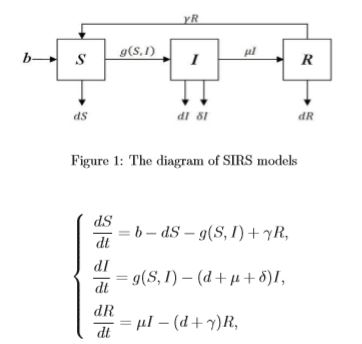
Equation 1. SIR Model is an ordinary differential equation model, and can be described by the above equation (source:
ASU
,
ASU Public Course
).

Parameters being used in the equation includes,

The infectious rate, β, controls the rate of spread which represents the probability of transmitting disease between a susceptible and an infectious individual.
D, the average duration, or say days of infection.
The recovery rate, γ = 1/D, is determined by the average duration.
N, the total population of the study.

Basic Reproduction Number

One of the critical question that epidemiologisits ask the most during each disease outbreak, is that how far and how fast a virus can spread through a population, and the basic reproduction number (a.k.a. the R naught, or R0) is often used to answer the question.

R0 refers to "how many other people one sick person is likely to infect on average in a group that's susceptible to the disease (meaning they don’t already have immunity from a vaccine or from fighting off the disease before)", and is "super important in the context of public health because it foretells how big an outbreak will be. The higher the number, the greater likelihood a large population will fall sick" [1].

Another mostly asked question is how contagious or deadly a virus is, and it together with R0 can depict the most important properties of a virus. Take Measles as an example, as the most contagious virus researchers know about, measles can linger in the air of a closed environment and sicken people up to two hours after an infected person who coughed or sneezed there has left. R0 of measles can be as high as 18, if people exposed to the virus aren't vaccinated. Let's now compare it to Ebola, which is more deadly but much less efficient in spreading. R0 of Ebola is typically just 2, which in part might be due to many infected individuals die before they can pass the virus to someone else.

How a `R0` is computed?

In a basic scenario, the basic reproductive number R0 equals to

R0 = β/γ = β*D

However, in a fully susceptible population, R0 is the number of secondary infections generated by the first infectious individual over the course of the infectious period, which is defined as,

R0=S*L*β

in which S=the number of susceptible hosts, L=length of infection, and β=transmissibility.

How to understand `R0`?

According to this heathline article, there are three possibilities for the potential spread or decline of a disease, depending on its R0 value:

If less than 1, each existing infection causes less than one new infection, and the disease will decline and eventually die out.
If equals to 1, each existing infection causes one new infection, and the disease will stay alive and stable, but there will not be an outbreak or an epidemic.
If more than 1, each existing infection causes more than one new infection, and the disease will spread between people, and there may be an outbreak or epidemic.

Fit the SIR Model per country

In order to fit the SIR model with the actual number of confirmed cases (and the recovered, and death tolls), we need to estimate the β and γ parameters. In the process, we will use solve_ivp function in scipy module, to solve the ordinary differential equation in the SIR model.

from scipy.integrate import solve_ivp
from scipy.optimize import minimize
from datetime import timedelta, datetime

"""The dict defined here includes the countries to run the model against,
   and the date that the first confirmed case was reported.
"""
START_DATE = {
  'China': '1/22/20',
  'Japan': '1/22/20',
  'Korea, South': '1/22/20',
  'US': '1/22/20',
  'Italy': '1/31/20',
  'Spain': '2/1/20',
  'Iran': '2/19/20'
}

# Adding into the consideration the social distancing factor (to be explained in the next section)
rho = 1

class Learner(object):
    """constructs an SIR model learner to load training set, train the model,
       and make predictions at country level.
    """
    def __init__(self, country, loss, start_date, predict_range,s_0, i_0, r_0):
        self.country = country
        self.loss = loss
        self.start_date = start_date
        self.predict_range = predict_range
        self.s_0 = s_0
        self.i_0 = i_0
        self.r_0 = r_0

    def load_confirmed(self, country):
      """
      Load confirmed cases downloaded from pre-made dataframe
      """
      country_df = world_confirmed_ts_df[world_confirmed_ts_df["Country/Region"] == country]
      return country_df.iloc[0].loc[START_DATE[country]:]

    def load_dead(self, country):
      """
      Load deaths downloaded from pre-made dataframe
      """
      country_df = world_deaths_ts_df[world_deaths_ts_df["Country/Region"] == country]
      return country_df.iloc[0].loc[START_DATE[country]:]

    def load_recovered(self, country):
      """
      Load recovered cases downloaded from pre-made dataframe
      """
      country_df = world_recovered_ts_df[world_recovered_ts_df["Country/Region"] == country]
      return country_df.iloc[0].loc[START_DATE[country]:]

    def extend_index(self, index, new_size):
        values = index.values
        current = datetime.strptime(index[-1], '%m/%d/%y')
        while len(values) < new_size:
            current = current + timedelta(days=1)
            values = np.append(values, datetime.strftime(current, '%m/%d/%y'))
        return values

    def predict_0(self, beta, gamma, data):
        """
        Simplifield version.
        Predict how the number of people in each compartment can be changed through time toward the future.
        The model is formulated with the given beta and gamma.
        """
        predict_range = 150
        new_index = self.extend_index(data.index, predict_range)
        size = len(new_index)
        def SIR(t, y):
            S = y[0]
            I = y[1]
            R = y[2]
            return [-rho*beta*S*I, rho*beta*S*I-gamma*I, gamma*I]
        extended_actual = np.concatenate((data.values, [None] * (size - len(data.values))))
        return new_index, extended_actual, solve_ivp(SIR, [0, size], [S_0,I_0,R_0], t_eval=np.arange(0, size, 1))
    
    def predict(self, beta, gamma, data, recovered, death, country, s_0, i_0, r_0):
        """
        Predict how the number of people in each compartment can be changed through time toward the future.
        The model is formulated with the given beta and gamma.
        """
        new_index = self.extend_index(data.index, self.predict_range)
        size = len(new_index)

        def SIR(t, y):
            S = y[0]
            I = y[1]
            R = y[2]
            return [-rho*beta*S*I, rho*beta*S*I-gamma*I, gamma*I]

        extended_actual = np.concatenate((data.values, [None] * (size - len(data.values))))
        extended_recovered = np.concatenate((recovered.values, [None] * (size - len(recovered.values))))
        extended_death = np.concatenate((death.values, [None] * (size - len(death.values))))
        solved = solve_ivp(SIR, [0, size], [s_0,i_0,r_0], t_eval=np.arange(0, size, 1))
        return new_index, extended_actual, extended_recovered, extended_death, solved

    def train_0(self):
        """
        Simplified version.
        Run the optimization to estimate the beta and gamma fitting the given confirmed cases.
        """
        data = self.load_confirmed(self.country)
        optimal = minimize(
            loss,
            [0.001, 0.001],
            args=(data),
            method='L-BFGS-B',
            bounds=[(0.00000001, 0.4), (0.00000001, 0.4)]
        )
        beta, gamma = optimal.x
        new_index, extended_actual, prediction = self.predict(beta, gamma, data)
        df = pd.DataFrame({
            'Actual': extended_actual,
            'S': prediction.y[0],
            'I': prediction.y[1],
            'R': prediction.y[2]
        }, index=new_index)
        fig, ax = plt.subplots(figsize=(15, 10))
        ax.set_title(self.country)
        df.plot(ax=ax)
        fig.savefig(f"{self.country}.png")
        
    def train(self):
        """
        Run the optimization to estimate the beta and gamma fitting the given confirmed cases.
        """
        recovered = self.load_recovered(self.country)
        death = self.load_dead(self.country)
        data = (self.load_confirmed(self.country) - recovered - death)

        optimal = minimize(loss, [0.001, 0.001], 
                           args=(data, recovered, self.s_0, self.i_0, self.r_0), 
                           method='L-BFGS-B', 
                           bounds=[(0.00000001, 0.4), (0.00000001, 0.4)])
        print(optimal)

        beta, gamma = optimal.x
        new_index, extended_actual, extended_recovered, extended_death, prediction = self.predict(beta, gamma, data, 
                                                                                                  recovered, death, 
                                                                                                  self.country, self.s_0, 
                                                                                                  self.i_0, self.r_0)
        df = pd.DataFrame({'Infected data': extended_actual, 'Recovered data': extended_recovered, 
                           'Death data': extended_death, 'Susceptible': prediction.y[0], 
                           'Infected': prediction.y[1], 'Recovered': prediction.y[2]}, index=new_index)

        fig, ax = plt.subplots(figsize=(15, 10))
        ax.set_title(self.country)
        df.plot(ax=ax)
        print(f"country={self.country}, beta={beta:.8f}, gamma={gamma:.8f}, r_0:{(beta/gamma):.8f}")
        fig.savefig(f"{self.country}.png")

We need to also define the loss function to be used in the optimization process - note that the the root mean squared error (RMSE) not only considers the confirmed cases, but also the recovered.

def loss(point, data, recovered, s_0, i_0, r_0):

    size = len(data)
    beta, gamma = point

    def SIR(t, y):
        S = y[0]
        I = y[1]
        R = y[2]
        return [-rho*beta*S*I, rho*beta*S*I-gamma*I, gamma*I]

    solution = solve_ivp(SIR, [0, size], [s_0,i_0,r_0], t_eval=np.arange(0, size, 1), vectorized=True)
    l1 = np.sqrt(np.mean((solution.y[1] - data)**2))
    l2 = np.sqrt(np.mean((solution.y[2] - recovered)**2))
    alpha = 0.1

    return alpha * l1 + (1 - alpha) * l2

Now let's run the estimation process against major countries suffering from the COVID-19 outbreak. The following cells illustrate how the number of the compartment can be changed over time, according to the SIR model.

How to decide the initial values of compartments? This is based on two conditions: the rough inference of the max quantity of susceptible people for each country, and the computation capacity (the execution takes overly long time for 1 million susceptible population). Though SIR model expects the susceptible to be homogenous, well-mixed, and accessible to each other, setting the whole population in the country is not realistic for sure. In this case, let's set the compartment 100000 to start with.

Also in the initial settings, the initial infectious people were 2 for every country, and the start of the outbreak is varied, as specified in the START_DATE dict object.

The initial batch of SIR Model fitting

countries = ['China', 'Korea, South']
predict_range = 250
s_0 = 100000
i_0 = 2
r_0 = 10

for country in countries:
    start_date = START_DATE[country]
    learner = Learner(country, loss, start_date, predict_range, s_0, i_0, r_0)
    learner.train()

      fun: 10280.378870137927
 hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
      jac: array([4227.74755862,   -7.67140591])
  message: b'ABNORMAL_TERMINATION_IN_LNSRCH'
     nfev: 375
      nit: 27
   status: 2
  success: False
        x: array([7.53235845e-06, 2.06861562e-02])
country=China, beta=0.00000753, gamma=0.02068616, r_0:0.00036413
      fun: 5302.062155691667
 hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
      jac: array([ 2.09337929e+08, -1.32026589e+03])
  message: b'CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH'
     nfev: 237
      nit: 19
   status: 0
  success: True
        x: array([1.01684995e-06, 4.17528180e-02])
country=Korea, South, beta=0.00000102, gamma=0.04175282, r_0:0.00002435

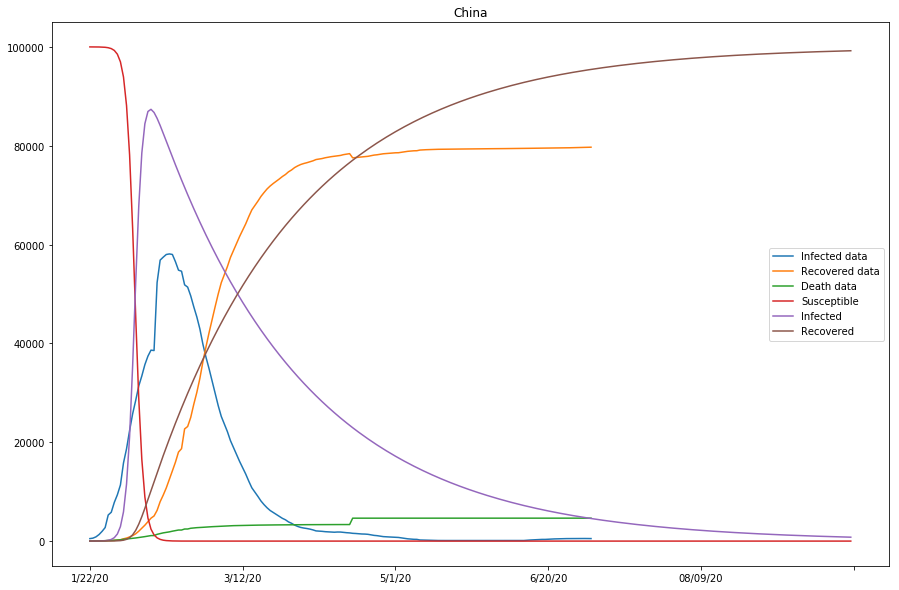
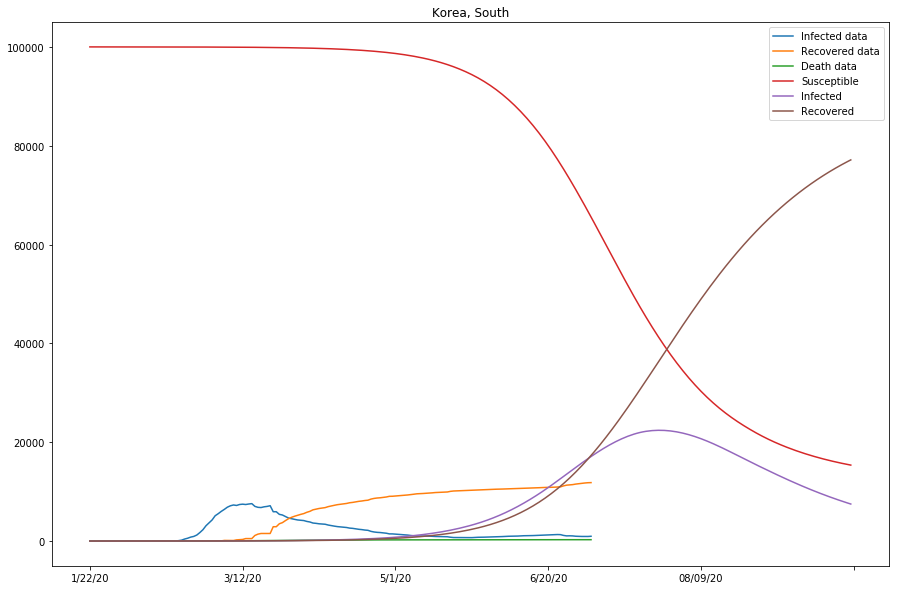
How do we decide if the model is a good approximation? First, by observing if curves of the Infected data and the projected Infected are close together; Second, by observing if the Recovered data and the projected Recovered curves are also close. For instance, in the previous cell output, we can see the approximation of the model is doing fairly nice for that of Mainland China, but not as ideal for that of South Korea.

countries = ['Japan', 'Italy', 'Spain']
predict_range = 250
s_0 = 100000
i_0 = 2
r_0 = 10

for country in countries:
    start_date = START_DATE[country]
    learner = Learner(country, loss, start_date, predict_range, s_0, i_0, r_0)
    learner.train()

      fun: 8039.341910449291
 hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
      jac: array([135990.51944766, -13777.95169901])
  message: b'CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH'
     nfev: 162
      nit: 6
   status: 0
  success: True
        x: array([4.45162819e-07, 4.45177249e-07])
country=Japan, beta=0.00000045, gamma=0.00000045, r_0:0.99996759
      fun: 42082.071337634945
 hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
      jac: array([1.38366158e+02, 1.67347025e-02])
  message: b'CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH'
     nfev: 399
      nit: 34
   status: 0
  success: True
        x: array([2.42577465e-06, 5.09067457e-02])
country=Italy, beta=0.00000243, gamma=0.05090675, r_0:0.00004765
      fun: 37210.55846013384
 hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
      jac: array([-4.30707999e+09,  1.31464732e+05])
  message: b'CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH'
     nfev: 297
      nit: 23
   status: 0
  success: True
        x: array([2.89569389e-06, 9.88570287e-02])
country=Spain, beta=0.00000290, gamma=0.09885703, r_0:0.00002929

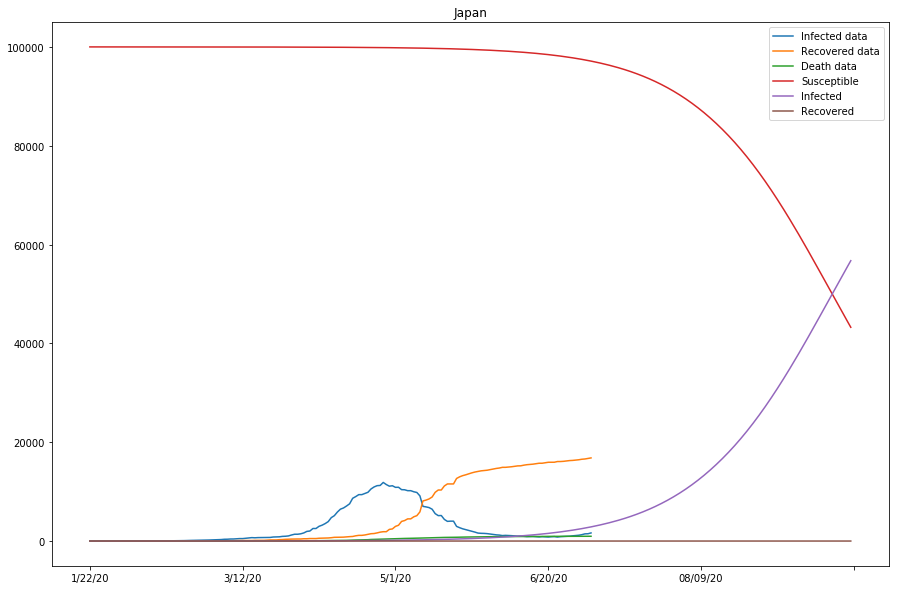
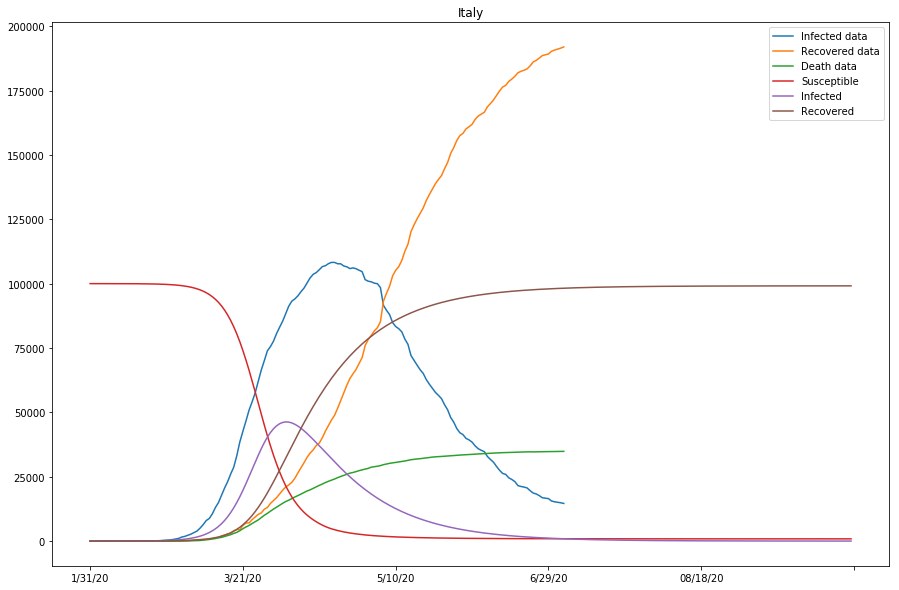
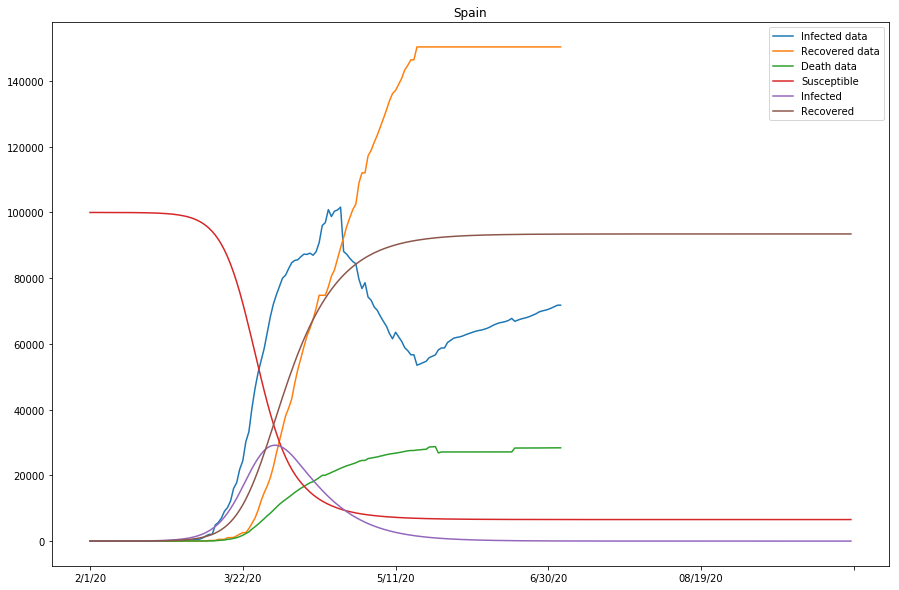
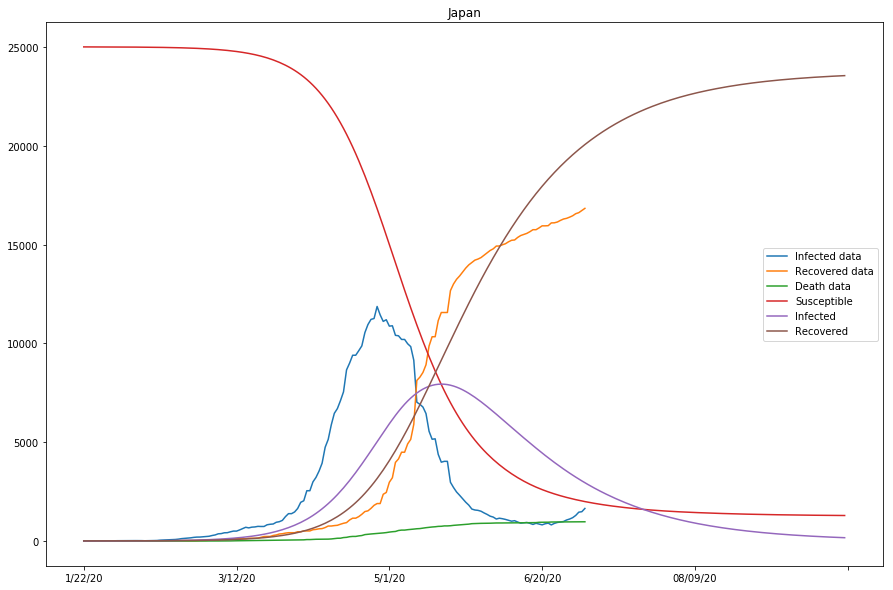
As seen in the cell output above, the approximation of the model is looking reasonably good for that of Italy and Spain, but not as ideal for that of Japan - the gap between the Infected data and the projected Infected curves is overly large, and so is that between the Recovered data and Recovered curves.

predict_range = 250
s_0 = 100000
i_0 = 2
r_0 = 10

country="US"
start_date = START_DATE[country]
learner = Learner(country, loss, start_date, predict_range, s_0, i_0, r_0)
learner.train()

      fun: 317178.7735714818
 hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
      jac: array([9.87201929, 0.20954758])
  message: b'CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH'
     nfev: 45
      nit: 5
   status: 0
  success: True
        x: array([0.02542935, 0.02778655])
country=US, beta=0.02542935, gamma=0.02778655, r_0:0.91516763

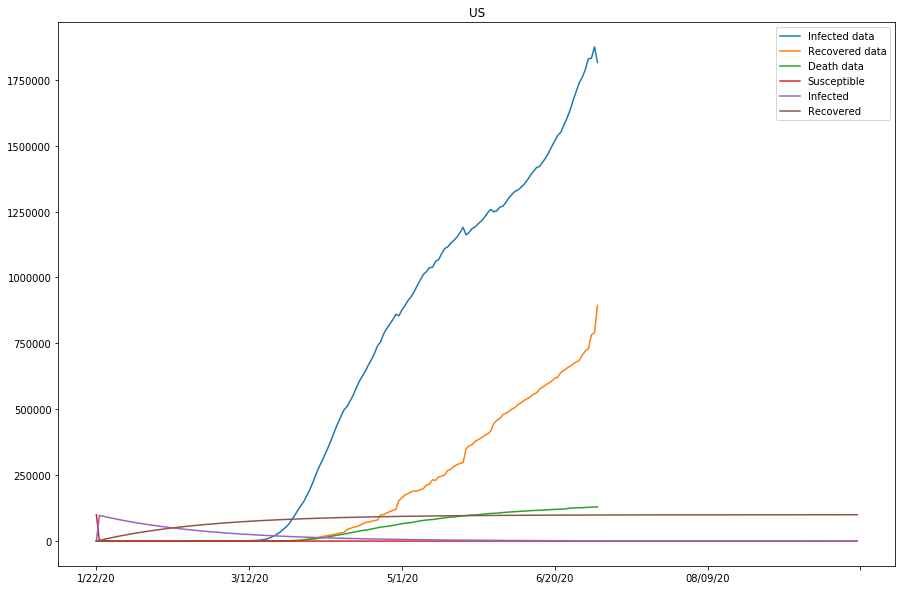
Table 3 (as shown below) displays what we have got so far with the model, for the studied countries. Note that the last column represents if the approximation of the model is good, or else parameters need to be modified before running the 2nd batch of fitting.

Countries	Beta	Gamma	R0	Good approximation?
China	0.00000753	0.02068616	0.00036413	True
Japan	0.00000045	0.00000045	0.9999675	False
S. Korea	0.00000102	0.04175282	0.00002435	False
Italy	0.00000243	0.05090675	0.00004765	True
Spain	0.00000290	0.09885703	0.00002929	True
US	0.02542935	0.02778655	0.91516763	False

Table 3. The computed Beta, Gamma, and R0 values for studied countries (with data collected up to EOD 07/04/2020).

Now the SIR model is well-fitting the actual data for both confirmed and recovered cases. The R0 values of Japan and the United States are significantly higher than in other countries, which might be caused by the relatively lower recovery rates in both countries, or that the initial values can be assumed wrong (or that the model fails to find the global minimum in the optimization process).

On the other hand, the total number of confirmed cases for the United States is way higher than the initial susceptible number we picked here. The trends for S, I, and R, and the R0 value hence computed would not make much sense. In the following cells, we will experiment with larger susceptible numbers (and/or longer prediction periods), and see how the results would differ.

The second batch of SIR Model fitting

Let's run the model again with modified parameters for the countries that (1) were showing unreasonably high R0 values, or (2) failed to make good approximation in the initial batch.

predict_range = 250
s_0 = 25000
i_0 = 2
r_0 = 10

country="Japan"
start_date = START_DATE[country]
learner = Learner(country, loss, start_date, predict_range, s_0, i_0, r_0)
learner.train()

      fun: 1422.4699520979984
 hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
      jac: array([279725.30349416,    589.61854847])
  message: b'CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH'
     nfev: 432
      nit: 16
   status: 0
  success: True
        x: array([5.16087340e-06, 4.11036952e-02])
country=Japan, beta=0.00000516, gamma=0.04110370, r_0:0.00012556

countries = ['Korea, South', 'US']
predict_range = 250
s_0_values = [25000, 1000000]
i_0 = 2
r_0 = 10

for country, s_0 in zip(countries, s_0_values):
    start_date = START_DATE[country]
    learner = Learner(country, loss, start_date, predict_range, s_0, i_0, r_0)
    learner.train()

      fun: 2177.392810393044
 hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
      jac: array([258762.58505377,    387.30468077])
  message: b'CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH'
     nfev: 315
      nit: 26
   status: 0
  success: True
        x: array([1.01798066e-05, 6.15592306e-03])
country=Korea, South, beta=0.00001018, gamma=0.00615592, r_0:0.00165366
      fun: 132485.37921448034
 hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
      jac: array([1.83150386e+10, 4.76380734e+06])
  message: b'ABNORMAL_TERMINATION_IN_LNSRCH'
     nfev: 300
      nit: 15
   status: 2
  success: False
        x: array([2.31863766e-07, 1.31293805e-01])
country=US, beta=0.00000023, gamma=0.13129380, r_0:0.00000177

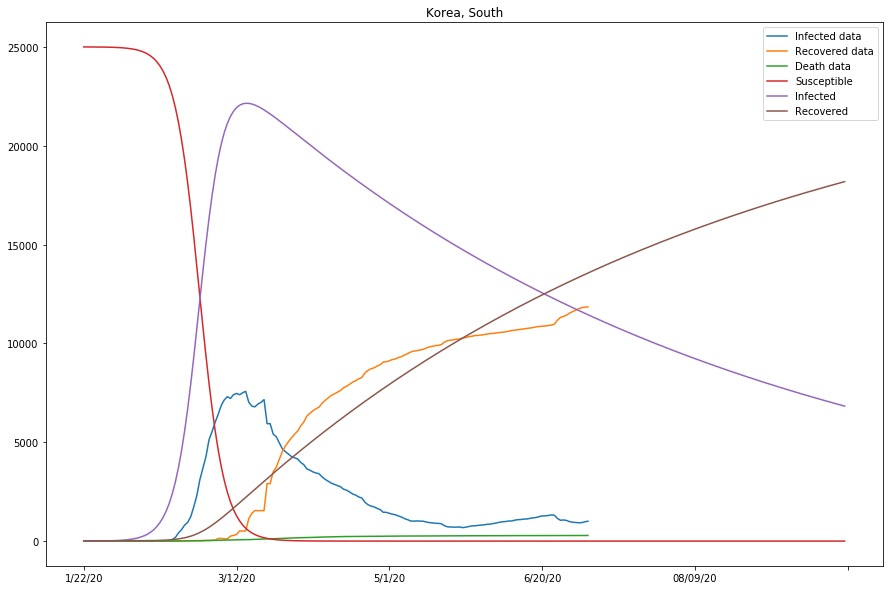
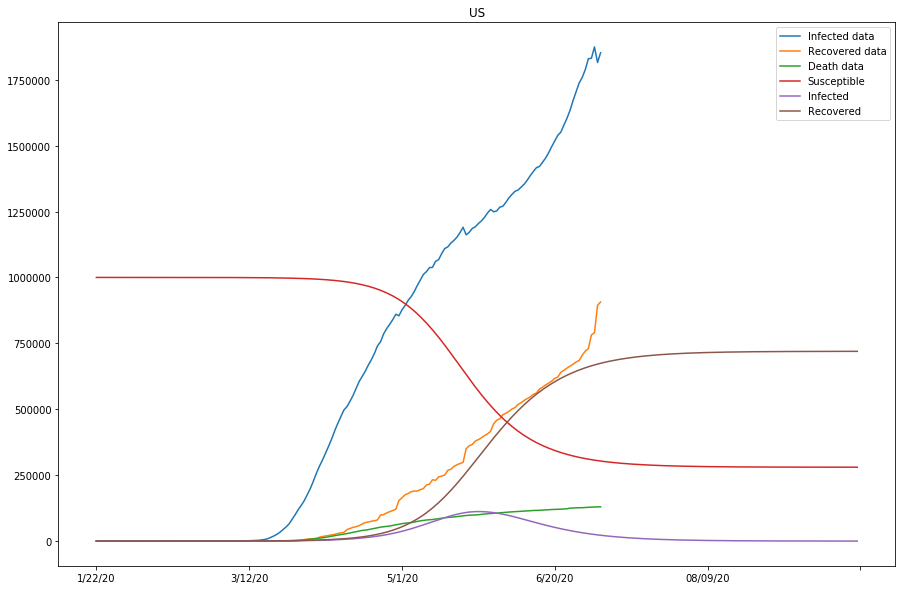
Table 4 (as shown below) lists the modified Beta, Gamma, and R0 values for Japan, Korea, Spain and US. Note that the last column represents if the approximation of the model is good, or else parameters need to be modified before the 3rd batch of fitting.

Countries	Beta	Gamma	R0	Good approximation?
China	0.00000753	0.02068616	0.00036413	True
Japan	0.00000516	0.04110370	0.00012556	True
S. Korea	0.00001018	0.00615592	0.00165366	True
Italy	0.00000243	0.05090675	0.00004765	True
Spain	0.00000290	0.09885703	0.00002929	True
US	0.00000023	0.13129380	0.00000177	False

Table 4. The Beta, Gamma, and R0 values computed out of the 2nd batch model fitting for studied countries (with data collected up to EOD 07/04/2020).

Up to this point, we have run two batches of SIR model fitting, and all countries of study except for the United States have shown good approximations to the model (with modified parameters). Because the susceptible values set for the United States so far have been too low compared to the actual confirmed cases, we are going to continue modifying the s_0 values for the United States, and see if by doing so, the approximation of the model fitting can be improved in the next section.

The final batch of SIR Model fitting

predict_range = 250
s_0 = 2000000
i_0 = 2
r_0 = 10

country="US"
start_date = START_DATE[country]
learner = Learner(country, loss, start_date, predict_range, s_0, i_0, r_0)
learner.train()

      fun: 273805.4913666793
 hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
      jac: array([ 1849.03037734, -1823.58780876])
  message: b'CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH'
     nfev: 30
      nit: 5
   status: 0
  success: True
        x: array([0.00161177, 0.00161186])
country=US, beta=0.00161177, gamma=0.00161186, r_0:0.99994539

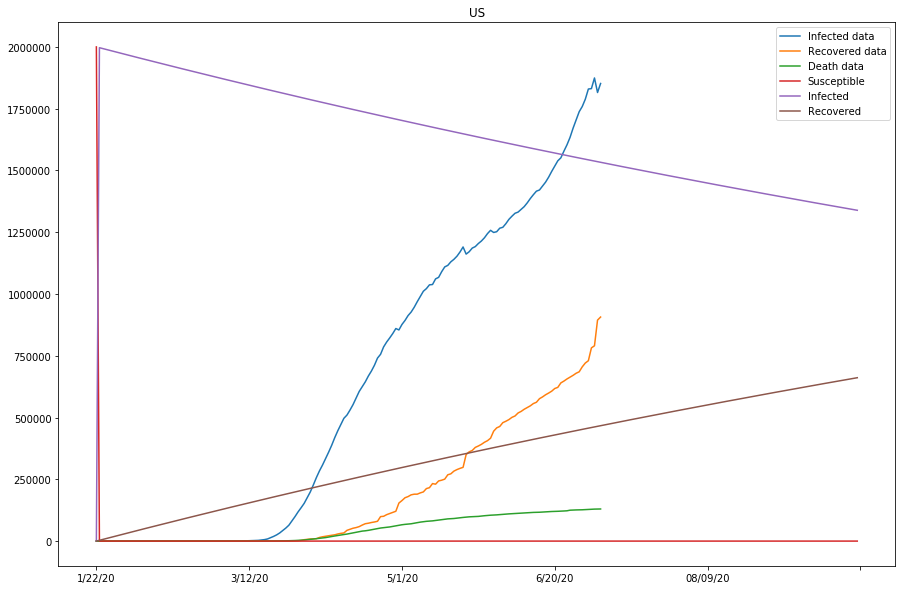
predict_range = 250
s_0 = 3000000
i_0 = 2
r_0 = 10

country="US"
start_date = START_DATE[country]
learner = Learner(country, loss, start_date, predict_range, s_0, i_0, r_0)
learner.train()

      fun: 361448.0875488295
 hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
      jac: array([3502.73912773,  -58.84794518])
  message: b'CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH'
     nfev: 24
      nit: 3
   status: 0
  success: True
        x: array([0.00099983, 0.00106169])
country=US, beta=0.00099983, gamma=0.00106169, r_0:0.94172925

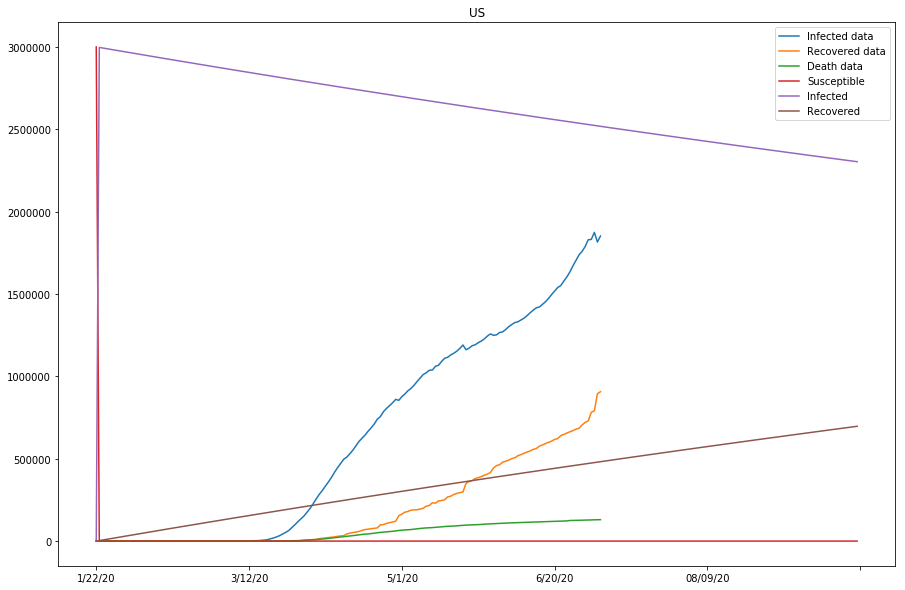
The previous two plots were due to susceptible being set too low, and we will continue to adjust the s_0 to larger numbers.

predict_range = 250
s_0 = 3500000
i_0 = 2
r_0 = 10

country="US"
start_date = START_DATE[country]
learner = Learner(country, loss, start_date, predict_range, s_0, i_0, r_0)
learner.train()

      fun: 224079.8306076969
 hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
      jac: array([ 3.91748893e+12, -2.12266260e+06])
  message: b'CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH'
     nfev: 207
      nit: 7
   status: 0
  success: True
        x: array([3.09456750e-08, 9.17191515e-03])
country=US, beta=0.00000003, gamma=0.00917192, r_0:0.00000337

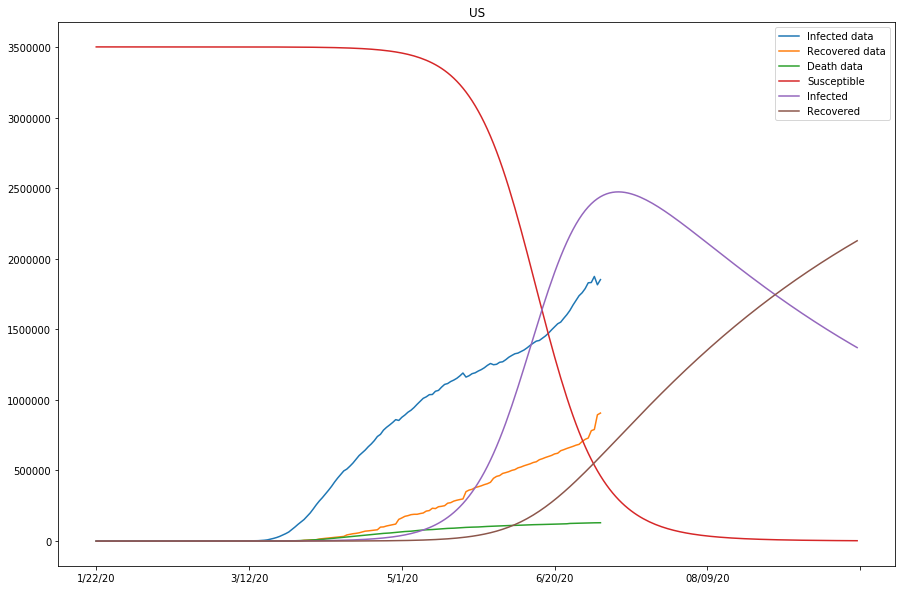
predict_range = 250
s_0 = 4000000
i_0 = 2
r_0 = 10

country="US"
start_date = START_DATE[country]
learner = Learner(country, loss, start_date, predict_range, s_0, i_0, r_0)
learner.train()

      fun: 369649.23863352626
 hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
      jac: array([ 7.68412486e+08, -1.60154421e+04])
  message: b'ABNORMAL_TERMINATION_IN_LNSRCH'
     nfev: 186
      nit: 4
   status: 2
  success: False
        x: array([1.72969697e-08, 1.72955155e-08])
country=US, beta=0.00000002, gamma=0.00000002, r_0:1.00008408

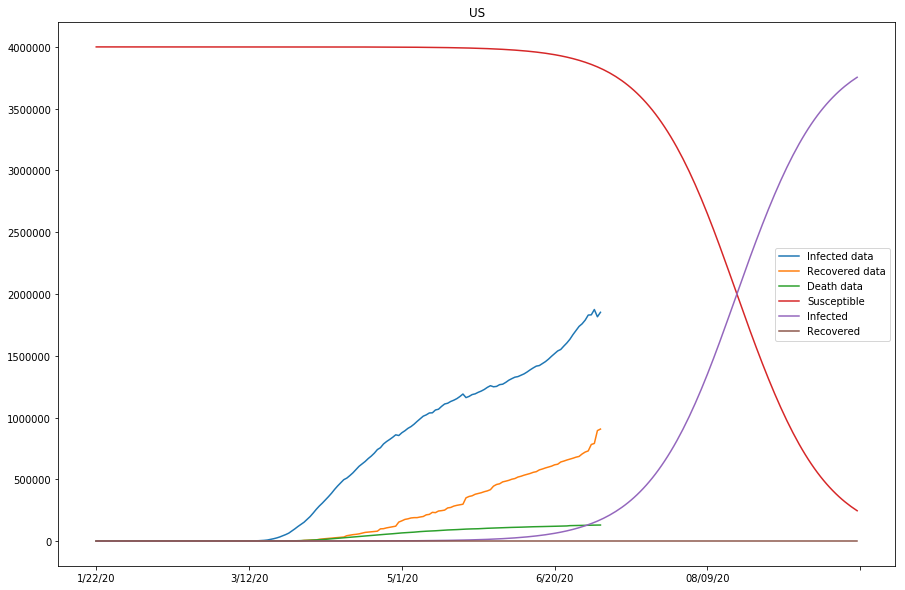
s_0	Beta	Gamma	R0	Date of Peak	Max Infected Population
0.1M	0.02542935	0.02778655	0.91516763	Not applicable	Not applicable
1M	0.00000023	0.13129380	0.00000177	Not applicable	Not applicable
2M	0.00161177	0.00161186	0.99994539	Not applicable	Not applicable
3M	0.00099983	0.00106169	0.94172925	Not applicable	Not applicable
3.5M	0.00000003	0.00917192	0.00000337	07/19/2020	2.5M
4M	0.00000002	0.00000002	1.00008408	>10/28/2020	>4M

Table 5. The Beta, Gamma, and R0 values computed out of the final batch model fitting for the United States (with data collected up to EOD 07/04/2020).

Efforts of social distancing can mitigate the spread of infectious disease, and impact the transmitting/infectious rate, β. Now, let's introduce this new value, ρ, to describe the social distancing effect. It is going to be ranging from 0 to 1, where 0 indicates everyone is locked down and quarantined (as individuals), and 1 is equivalent to the base case demonstrated above. With ρ being defined, the SIR model will be modified as:

S' = -ρ*β*S*I

We have already seen the trends of SIR model fitting when ρ=1. Now, let's set ρ to 0.8, and 0.5, and see the flattening effect as the social distancing effects got increased to contain the disease over a set period of time.

rho = 0.8

predict_range = 250
s_0 = 3500000
i_0 = 2
r_0 = 10

country="US"
start_date = START_DATE[country]
learner = Learner(country, loss, start_date, predict_range, s_0, i_0, r_0)
learner.train()

      fun: 254442.13493214428
 hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
      jac: array([4.47150648e+12, 5.36130878e+06])
  message: b'ABNORMAL_TERMINATION_IN_LNSRCH'
     nfev: 288
      nit: 5
   status: 2
  success: False
        x: array([3.81849319e-08, 1.66008689e-02])
country=US, beta=0.00000004, gamma=0.01660087, r_0:0.00000230

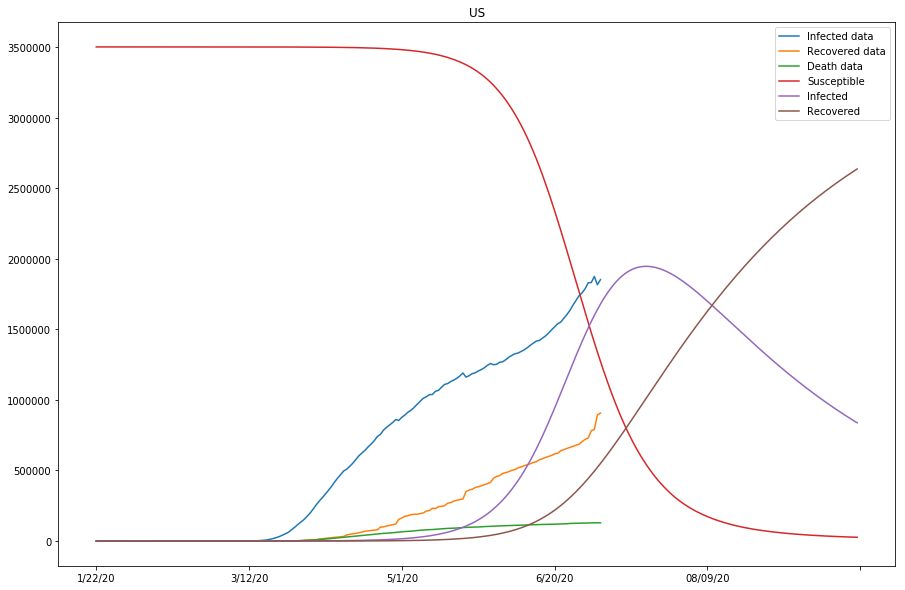
As listed in Table 6, social distancing efforts will likely improve the survivability of the disease by giving more time for treatments and supplies to develop while keeping the peaks low.

Rho	Beta	Gamma	R0	Date of Peak	Max Infected Population
1	0.00000003	0.00917192	0.00000337	07/19/2020	2.5M
0.8	0.00000004	0.01660087	0.00000230	07/26/2020	1.95M

Table 6. The Beta, Gamma, and R0 values computed with different `Rho` factors (when `S`=3.5M) for the United States (with data collected up to EOD 07/04/2020).

Comparison between models

The SIR model we have been seeing so far, is a simplified approximation of early dynamics of an epidemic, with exponential growth. Based on a system of differential equations and three distinct populations (S, I, and R), it has been around for decades. For future extensions of this study, we can explore other complex approaches, such as the SEIR model (an adaptation of SIR with an additional population of Exposed individuals), or a polynomial curve fitting further-along epidemics and recalibrating locally, for instance, the CHIME model.

Category	SIR	SEIR [18]	CHIME [18]
Definition	Simple & Basic compartmental model	a derivative of SIR model that contains `exposed` (infected but not infectious)	COVID19 Hospital Impact Model for Epidemics
Latency Period	No	Yes	No
Progress of Individuals	S-I-R	S-E-I-R	S-I-R
Examples	N = S+I+R	N = S+E+I+R	N = S+I+R

Conclusions

Before vaccines to COVID-19 come available to all, what governments can do is only to slow down the transmission. By doing so, we don’t actually stop the spread but keep the transmission and the active cases at a point that in the time being well within the limits of the handling capacity of medical facilities. This is what we call as Flattening The Curve. As advised by experts, there are at least three measures to help flatten the curve:

Place travel restrictions; the transmission could be reduced by restricting people from traveling in or out of a particular region with high infections.
Keep social distance; As shown in the SIR modeling that COVID-19 has a high R0 and each infected person ends up infecting 2 or 3 people, social distancing might be the most significant in reducing transmission from the infected to the others.
Have more testing done. Testing is necessary to quickly identify and isolate the infected from the non-infected given that Covid-19 has a long incubation period (ranging from 2 to 26 days, while symptoms usually start appearing after 5-7 days), it is possible for an infected individual to spread the infection to others without his/her even knowing.

As stated by Thomas Pueyo in his Medium Post (which can be seen in the illustration below), when combining Transmission reduction and Travel restriction, if transmission rate of COVID-19 went down by even 25%, it could delay the peak by almost 14 weeks. Further reduction would delay it even more.

Together with what we have seen from the SIR modeling, reducing the transmission rate, and keeping the number of compartment small is crucial to flattening the curve. All should act together and fight the pandemic!